Figure 1:Acumulado de precipitación en el radar de Guaviare

Estimación Cuantitativa de la Lluvia¶

Introducción¶

En este cuadernillo aprenderás cómo estimar la lluvia acumulada (QPE, Quantitative Precipitation Estimation) a partir de datos de reflectividad. Usaremos una relación empírica Z–R para convertir reflectividad en tasa de precipitación, y luego integraremos en el tiempo para obtener acumulados.

Los datos provienen del radar meteorológico ubicado en Guaviare, Colombia, y están preprocesados en formato Zarr siguiendo los principios FAIR.

📚 Descripción general¶

✔ Cómo aplicar relaciones Z–R para estimar lluvia a partir de reflectividad
✔ Cómo calcular acumulados de precipitación sobre tiempo con datos radar
✔ Cómo visualizar mapas de lluvia en 2D usando xarray y matplotlib
✔ Cómo usar datos radar del radar Guaviare desde Zarr en la nube

✅ Requisitos previos¶

Conceptos	Importancia	Notas
Xarray	Necesario	Manipulación de datos multidimensionales
Radar meteorológico	Necesario	Interpretación física de reflectividad (dBZ)
Dask	Útil	Procesamiento paralelo de grandes volúmenes

Tiempo de aprendizaje: 40 minutos
Requisitos del sistema:
- Python 3.9+
- 4 GB RAM mínimo
- Conexión a internet para acceso a datos en Jetstream 2

Librerías¶

Importamos las librerías necesarias para este cuaderno.

# Manipulación de datos
import numpy as np
import xarray as xr

# Visualización
import matplotlib.pyplot as plt

# Computación distribuida
from dask.distributed import Client, LocalCluster

⏱️ Tiempo estimado de aprendizaje:

📖 Lectura y ejecución: 30–40 minutos

✍️ Formato: interactivo

1. Fundamento: Estimación Cuantitativa de Precipitación (QPE)¶

La estimación cuantitativa de precipitación (QPE) consiste en transformar la reflectividad medida por el radar (en unidades dBZ) a una tasa de precipitación (mm/h), usando una relación empírica del tipo:

Z = a \cdot R^b

(1)

Una de las más utilizadas es la relación de Marshall y Palmer (1948):

Z = 200 \cdot R^ {1.6}

(2)

from dask.distributed import Client, LocalCluster

# Create a local cluster with correct arguments
cluster = LocalCluster(
    n_workers=4,              # Number of worker processes
    memory_limit='2GB'        # Per worker memory limit
)

client = Client(cluster)
client

2. Acceso a datos del radar de Guaviare¶

En esta sección accederemos a datos del radar meteorológico ubicado en San José del Guaviare, Colombia. Estos datos han sido preprocesados y almacenados en formato Zarr v3, siguiendo los principios FAIR (Findable, Accessible, Interoperable, Reusable), y se encuentran disponibles públicamente a través del servicio en la nube Jetstream 2.

Usaremos xarray y fsspec


# URL del endpoint S3 en Jetstream 2
url = "https://js2.jetstream-cloud.org:8001/"
path = "s3://pythia/radar/AtmosCol2025/Guaviare.zarr"

# Abrir el DataTree del radar
dtree = xr.open_datatree(
    path,
    # "/media/alfonso/drive/Alfonso/python/raw2zarr/zarr/Guaviare.zarr",
    engine="zarr",
    chunks={},
    backend_kwargs={
        "consolidated": False,
        "storage_options": {
            "anon": True,
            "client_kwargs": {
                "endpoint_url": url,
            },
        },
    },
)

#display(dtree)

2.1 Exploración de la estructura del volumen radar¶

El radar de San José del Guaviare contiene múltiples modos de escaneo organizados como grupos dentro del DataTree, tales como PRECA, PRECB, PRECC y SURVP. Cada uno corresponde a una configuración de volumen distinta en el modo de precipitación.

Dentro de cada grupo se encuentran:

Variables globales (latitude, longitude, altitude, etc.)
Subgrupos de barrido (sweep_0, sweep_1, sweep_2, ...)
Parámetros del radar (radar_parameters)
Correcciones de georreferenciación (georeferencing_correction)

list(dtree.children)

['PRECA', 'PRECC', 'SURVP', 'PRECB']

Y los nodos hijos dentro de un volumen específico, por ejemplo PRECA:

list(dtree["PRECA"].children)

['georeferencing_correction',
 'sweep_3',
 'radar_parameters',
 'sweep_0',
 'sweep_2',
 'sweep_1']

dtree["/PRECA/sweep_0/DBZH"]

3. Cálculo de la precipitación acumulada¶

En esta sección estimaremos la profundidad de precipitación acumulada usando la reflectividad radar de Guaviare y una relación empírica tipo ( Z = a \cdot R^b ). Para ello, aplicaremos la fórmula de Marshall y Palmer y realizaremos una integración temporal sobre cada píxel.

La función rain_depth() implementa este proceso completo de forma vectorizada usando xarray.

3.1 Definición de la función `rain_depth`¶

def rain_depth(
    z: xr.DataArray, a: float = 200.0, b: float = 1.6, t: int = 5
) -> xr.DataArray:
    """
    Estima la profundidad de precipitación acumulada a partir de la reflectividad radar.

    Parámetros
    ----------
    z : xr.DataArray
        Reflectividad en dBZ o Z lineal (se determina automáticamente por las unidades).
    a : float, opcional
        Parámetro 'a' en la relación Z-R. Valor por defecto: 200.0.
    b : float, opcional
        Parámetro 'b' en la relación Z-R. Valor por defecto: 1.6.
    t : int, opcional
        Intervalo de tiempo en minutos entre volúmenes. Default: 5.

    Retorna
    -------
    xr.DataArray
        Profundidad de lluvia estimada (en mm) por píxel.
    """
    # Revisión de unidades
    units = z.attrs.get("units", "")

    # Convertimos dBZ a Z lineal si es necesario
    if units.startswith("dB"):
        z_lin = 10 ** (z / 10)
    else:
        z_lin = z  # ya está en unidades lineales

    # Aplicamos la relación Z-R e integramos en el tiempo
    r = ((1 / a) ** (1 / b)) * z_lin ** (1 / b)
    return r * (t / 60)  # profundidad acumulada en mm

3.2 Aplicación sobre datos del radar Guaviare (`SURVP/sweep_0`)¶

Usamos el barrido más bajo (sweep_0) del volumen SURVP, que corresponde a una elevación cercana a (0.5^\circ), ideal para estimar precipitación acumulada sobre la superficie.

Seleccionamos la reflectividad horizontal (DBZH) y aplicamos la función rain_depth.

# Selección del barrido y variable de reflectividad
ref_log = dtree["/SURVP/sweep_0/DBZH"]

# Cálculo de la precipitación acumulada (en mm) para cada volumen
rr = rain_depth(ref_log)

rr

3.3 Estimación de la lluvia total acumulada¶

Una vez calculada la tasa de precipitación para cada volumen, podemos estimar la lluvia total acumulada del evento sumando a lo largo del tiempo (vcp_time).

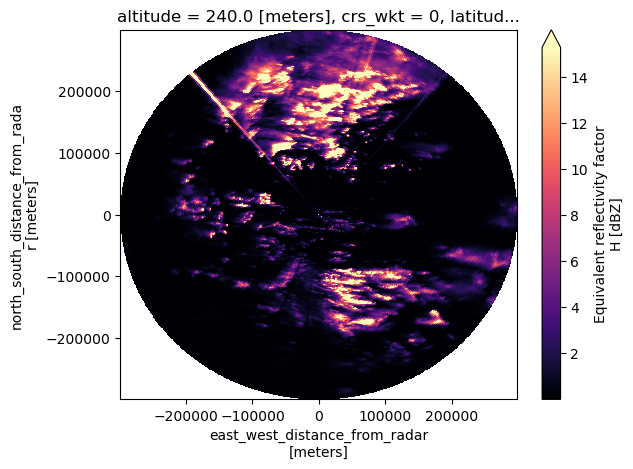
rr_total = rr.sum(dim="vcp_time", skipna=True)

rr_total

Visualizamos el campo acumulado:

%%time
rr_total.plot(x="x", y="y", cmap="magma", robust=True);

CPU times: user 1.8 s, sys: 372 ms, total: 2.17 s
Wall time: 38.6 s

3.4 Acumulaciones parciales por intervalo de tiempo¶

El volumen radar cubre el periodo:

Inicio: 2025-06-19 18:19 UTC
Fin: 2025-06-19 23:50 UTC

A continuación, estimaremos la lluvia acumulada para distintos intervalos:

Primera hora del evento
Primeras dos horas
Evento completo

# Conversión explícita a datetime64 para selección

t0 = np.datetime64("2025-06-19T18:19:00")
t1 = np.datetime64("2025-06-19T19:19:00")
t2 = np.datetime64("2025-06-19T20:19:00")

# Subconjuntos únicos para cada intervalo
rr_sel_1h = rr.sel(vcp_time=slice(t0, t1))
rr_sel_2h = rr.sel(vcp_time=slice(t1, t2))
rr_sel_remain = rr.sel(vcp_time=slice(t2, None))

# Acumulaciones parciales
rr_1h = rr_sel_1h.sum("vcp_time")
rr_2h = rr_1h + rr_sel_2h.sum("vcp_time")
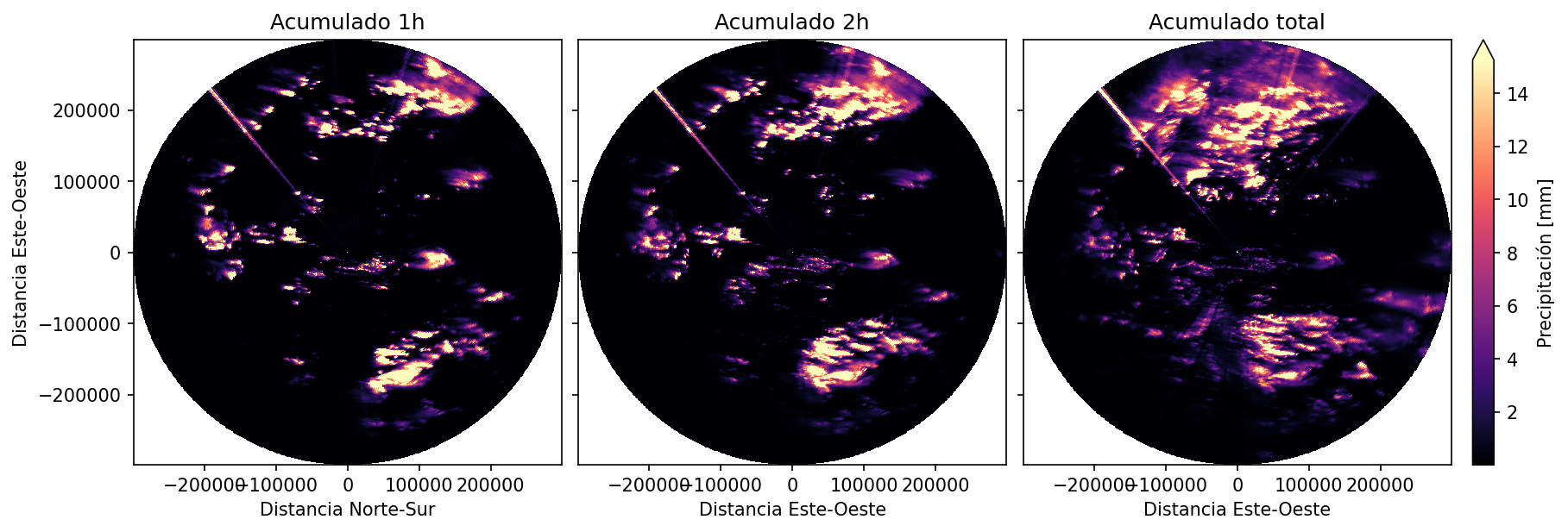
rr_total =  rr_2h + rr_sel_remain.sum("vcp_time")

3.5 Visualización de acumulaciones en distintos intervalos¶

A continuación, mostramos la estimación de lluvia acumulada para:

Primer hora
Primeras dos horas
Evento completo

%%time
fig, axs = plt.subplots(1, 3, figsize=(12, 4), constrained_layout=True, sharey=True)

# Primer hora
rr_1h.plot(
    ax=axs[0],
    cmap="magma",
    robust=True,
    x="x",
    y="y",
    add_colorbar=False, 
)

axs[0].set_title("Acumulado 1h")
axs[0].set_xlabel("Distancia Norte-Sur")
axs[0].set_ylabel("Distancia Este-Oeste")
# Dos horas
rr_2h.plot(
    ax=axs[1],
    cmap="magma",
    robust=True,
    x="x",
    y="y",
   add_colorbar=False, 
)

axs[1].set_title("Acumulado 2h")
axs[1].set_ylabel("")
axs[1].set_xlabel("Distancia Este-Oeste")
# Evento completo
rr_total.plot(
    ax=axs[2],
    cmap="magma",
    robust=True,
    x="x",
    y="y",
    cbar_kwargs={"label": "Precipitación [mm]"},
)
axs[2].set_title("Acumulado total")
axs[2].set_ylabel("")
axs[2].set_xlabel("Distancia Este-Oeste")

plt.savefig("../images/qpe-car.png", dpi=150, bbox_inches='tight')
plt.show()

CPU times: user 7.08 s, sys: 852 ms, total: 7.93 s
Wall time: 1min 23s

4. Resumen¶

En este cuaderno aprendiste los fundamentos de la estimación cuantitativa de precipitación (QPE) usando datos de radar meteorológico. Los conceptos clave incluyen:

Las relaciones empíricas Z-R (como Marshall-Palmer) permiten convertir reflectividad medida en tasas de precipitación, aunque introducen incertidumbre debido a la variabilidad de distribuciones de gotas
La integración temporal de tasas instantáneas produce acumulados de profundidad útiles para hidrología y alertas tempranas
Los datos en formato Zarr en la nube permiten análisis eficientes sin descargas masivas, facilitando aplicaciones en tiempo real
La visualización espacial de acumulados revela patrones de precipitación que serían invisibles en datos puntuales de pluviómetros

Estas habilidades son fundamentales para monitoreo hidrológico, validación de modelos numéricos de predicción, y sistemas de alerta temprana de inundaciones en regiones tropicales.

¿Qué sigue?¶

Con estas habilidades de QPE, puedes explorar:

Perfiles Cuasi-Verticales (QVPs) - Analiza la estructura vertical de precipitación para identificar procesos microfísicos como fusión de nieve y crecimiento de granizo
Acceso a datos de radares - Aprende a trabajar con otros radares de la red colombiana (Carimagua, Barrancabermeja, etc.)
Datos de estaciones IDEAM - Compara estimaciones radar con mediciones de pluviómetros para validación

Proyecto sugerido¶

Desarrolla un sistema de validación de QPE:

Descarga datos de pluviómetros cercanos al radar de Guaviare desde el IDEAM
Extrae la serie temporal de precipitación radar en las ubicaciones de los pluviómetros
Calcula métricas de error: sesgo, RMSE, correlación
Investiga si otra relación Z-R reduce el error sistemático

Este proyecto te introducirá a las técnicas operacionales de calibración de radar usadas por servicios meteorológicos nacionales.

Referencias y recursos¶

Publicaciones científicas¶

Marshall, J. S., & Palmer, W. M. (1948). The distribution of raindrops with size. Journal of Meteorology, 5(4), 165-166. Marshall & Palmer (1948)
Rosenfeld, D., Wolff, D. B., & Atlas, D. (1993). General probability-matched relations between radar reflectivity and rain rate. Journal of Applied Meteorology, 32(1), 50-72.
Fulton, R. A., Breidenbach, J. P., Seo, D. J., Miller, D. A., & O’Bannon, T. (1998). The WSR-88D rainfall algorithm. Weather and Forecasting, 13(2), 377-395.

Recursos técnicos¶

Xradar Documentation - Lectura y procesamiento de datos de radar meteorológico
wradlib Documentation - Biblioteca completa para procesamiento de radar incluyendo correcciones de atenuación y beam blockage
PyART User Guide - Toolkit del ARM para algoritmos avanzados de radar
Jetstream2 Cloud Storage - Infraestructura de datos en la nube utilizada en este cuaderno

Datos¶

Proveedor: IDEAM (Instituto de Hidrología, Meteorología y Estudios Ambientales de Colombia)
Radar: San José del Guaviare (Guaviare, Colombia)
Almacenamiento: Project Pythia Jetstream 2 Object Store
Formato: Zarr v3 (ARCO - Analysis Ready, Cloud Optimized)
Ruta: s3://pythia/radar/AtmosCol2025/Guaviare.zarr

Agradecimientos¶

Este cuaderno utiliza:

Infraestructura de cómputo y almacenamiento de Project Pythia y NSF ACCESS (Jetstream 2)
Datos radar provistos por IDEAM Colombia
Procesamiento con raw2zarr (herramienta de conversión RAWDSX2 a Zarr)

References¶

Marshall, J. S., & Palmer, W. M. K. (1948). THE DISTRIBUTION OF RAINDROPS WITH SIZE. Journal of Meteorology, 5(4), 165–166. https://doi.org/10.1175/1520-0469(1948)005<;0165:tdorws>2.0.co;2

Estimación Cuantitativa de la Lluvia

Estimación Cuantitativa de la Lluvia¶

Introducción¶

📚 Descripción general¶

✅ Requisitos previos¶

Librerías¶

1. Fundamento: Estimación Cuantitativa de Precipitación (QPE)¶

2. Acceso a datos del radar de Guaviare¶

2.1 Exploración de la estructura del volumen radar¶

3. Cálculo de la precipitación acumulada¶

3.1 Definición de la función rain_depth¶

3.2 Aplicación sobre datos del radar Guaviare (SURVP/sweep_0)¶

3.3 Estimación de la lluvia total acumulada¶

3.4 Acumulaciones parciales por intervalo de tiempo¶

3.5 Visualización de acumulaciones en distintos intervalos¶

4. Resumen¶

¿Qué sigue?¶

Proyecto sugerido¶

Referencias y recursos¶

Publicaciones científicas¶

Recursos técnicos¶

Datos¶

Agradecimientos¶

3.1 Definición de la función `rain_depth`¶

3.2 Aplicación sobre datos del radar Guaviare (`SURVP/sweep_0`)¶