
Introducción a NumPy¶
NumPy (Numerical Python) es una librería fundamental para el análisis numérico y científico en Python.
Esta guía práctica está diseñada para que te familiarices con la sintaxis, funcionalidades básicas y buenas prácticas al trabajar con NumPy. Los conceptos aquí presentados serán esenciales para el uso posterior de librerías como Pandas y Xarray.
📚 Descripción general¶
En este cuaderno aprenderás los fundamentos de NumPy, la biblioteca base para computación científica en Python. NumPy proporciona arreglos multidimensionales eficientes y funciones matemáticas de alto rendimiento que son esenciales para el análisis de datos científicos. Dominarás la creación, manipulación y operación con arreglos, así como técnicas de indexación, broadcasting y funciones estadísticas.
✅ Requisitos previos¶
| Concepto | Importancia | Notas |
|---|---|---|
| Introducción a Python | Necesario | Tipos de datos, funciones, operadores |
| Introducción a JupyterLab | Necesario | Navegación y ejecución de celdas |
| NumPy (Pythia Foundations) | Complementario | Lectura sugerida para profundizar |
⏱️ Tiempo estimado de aprendizaje: 20–25 minutos
✍️ Formato: interactivo, ejecuta y modifica el código a medida que avanzas
1. ¿Qué es NumPy?¶
NumPy es una librería para el cálculo numérico que permite trabajar con arreglos multidimensionales, de forma eficiente y vectorizada.
Ventajas:
Velocidad (optimizado en C)
Menos líneas de código
Funciones estadísticas, álgebra lineal, etc.
2. Creación de arreglos (arrays)¶
Los arreglos —en inglés arrays— son la estructura de datos fundamental en NumPy. Funcionan de manera similar a las listas en Python, pero están optimizados para realizar operaciones matemáticas de forma eficiente y vectorizada.
Puedes crear un arreglo a partir de una lista de Python utilizando la función np.array():
import numpy as np
a = np.array([1, 2, 3])print(a)
print("Tipo:", type(a))
print("Dimensiones:", a.ndim)
print("Forma:", a.shape)
print("Tipo de datos:", a.dtype)[1 2 3]
Tipo: <class 'numpy.ndarray'>
Dimensiones: 1
Forma: (3,)
Tipo de datos: int64
En este ejemplo:
type(a)nos indica que estamos trabajando con un objetondarrayndimnos da el número de dimensiones (1D, 2D, etc.)shapemuestra el tamaño de cada dimensióndtypeindica el tipo de dato contenido en el array (por ejemplo,int64,float32, etc.)
Este es el primer paso fundamental para comenzar a trabajar con datos numéricos en Python.
2.1 Arreglos bidimensionales (matrices 2D)¶
Los arreglos pueden tener más de una dimensión. En el caso de dos dimensiones, se les conoce comúnmente como matrices (2D arrays), y son muy útiles para representar datos tabulares o imágenes, por ejemplo.
Puedes crear una matriz a partir de una lista de listas:
matriz = np.array([[1, 2], [3, 4]])
print(matriz)[[1 2]
[3 4]]
Aquí estamos creando un arreglo de forma (2, 2), es decir, 2 filas y 2 columnas. Puedes inspeccionar sus propiedades igual que antes:
print("Dimensiones:", matriz.ndim)
print("Forma:", matriz.shape)
print("Tipo de datos:", matriz.dtype)Dimensiones: 2
Forma: (2, 2)
Tipo de datos: int64
Este tipo de estructura es esencial para realizar operaciones lineales y muchas tareas científicas donde los datos tienen más de una dimensión.
2.2 Generación automática de datos¶
NumPy nos ofrece funciones para crear arreglos de forma automática, sin necesidad de escribir cada valor manualmente. Estas funciones son muy útiles para generar rangos numéricos, vectores espaciados o arreglos inicializados con ceros o unos.
🔁 np.arange()¶
Crea un arreglo con valores numéricos espaciados de forma regular. Similar a la función range() de Python.
np.arange(0, 10, 2)array([0, 2, 4, 6, 8])Significado:
inicio = 0,fin = 10(excluyente),paso = 2Resultado:
[0 2 4 6 8]
📏 np.linspace()¶
Crea un arreglo con valores espaciados de forma uniforme en un intervalo definido.
np.linspace(1, 10, 5)array([ 1. , 3.25, 5.5 , 7.75, 10. ])Significado:
Crea 5 valores igualmente distribuidos entre 1 y 10 (inclusive)
⬛ np.zeros() y np.ones()¶
Crea arreglos de ceros o unos con una forma dada. Son útiles para inicializar estructuras.
np.zeros((2, 3)) # Matriz 2x3 llena de cerosarray([[0., 0., 0.],
[0., 0., 0.]])
np.ones((3, 2)) # Matriz 3x2 llena de unosarray([[1., 1.],
[1., 1.],
[1., 1.]])🏋️ Práctica: Creación de arreglos¶
Ahora es tu turno de practicar lo aprendido:
Crea un arreglo con las temperaturas máximas de una semana en Bogotá:
[18, 22, 25, 23, 19, 17, 20]Crea una matriz 3×3 con valores del 1 al 9 usando
np.arange()yreshape()Genera un arreglo de 10 valores espaciados uniformemente entre 0 y 100 usando
np.linspace()Crea una matriz de 2×4 llena de ceros
Estas funciones permiten crear estructuras base que luego se pueden modificar, poblar o usar como plantillas para cálculos más complejos.
3. Operaciones matemáticas básicas¶
En esta sección aprenderás a aplicar operaciones matemáticas directamente sobre arreglos de NumPy. Este tipo de operaciones vectorizadas permiten trabajar de forma eficiente con grandes volúmenes de datos sin necesidad de usar bucles.
3.1. Operaciones aritméticas básicas ➕➖✖️➗¶
Las operaciones como suma, resta, multiplicación y división se realizan elemento a elemento (element-wise), siempre que los arreglos tengan la misma forma (shape).
a = np.array([1, 2, 3])
b = np.array([10, 20, 30])
a, b(array([1, 2, 3]), array([10, 20, 30]))Ambos arreglos tienen una forma (3,), es decir, un vector unidimensional de tres elementos. Por tanto, podemos sumarlos o multiplicarlos directamente:
print("Suma:", a + b)
print("Resta:", a - b)
print("Multiplicación:", a * b)
print("División:", a / b)Suma: [11 22 33]
Resta: [ -9 -18 -27]
Multiplicación: [10 40 90]
División: [0.1 0.1 0.1]
⚠️ Si los arreglos tienen formas incompatibles, NumPy no podrá aplicar las operaciones directamente y generará un error, a menos que se aplique broadcasting.
3.2. Potencias y funciones matemáticas 🧮¶
NumPy incluye funciones para cálculo exponencial, raíces cuadradas, logaritmos, funciones trigonométricas, entre otras.
a = np.array([0, np.pi/2, np.pi])
print("Valores en radianes:", a)Valores en radianes: [0. 1.57079633 3.14159265]
print("Seno:", np.sin(a))
print("Coseno:", np.cos(a))
print("Exponencial:", np.exp([1, 2]))Seno: [0.0000000e+00 1.0000000e+00 1.2246468e-16]
Coseno: [ 1.000000e+00 6.123234e-17 -1.000000e+00]
Exponencial: [2.71828183 7.3890561 ]
También puedes redondear los valores o aplicar funciones estadísticas como suma total:
valores = np.cos(a)
print("Redondeo:", np.round(valores, 2))
print("Suma total:", np.sum(valores))Redondeo: [ 1. 0. -1.]
Suma total: 0.0
Estas herramientas serán fundamentales para el análisis numérico en climatología, física y otras ciencias.
4. Indexado y selección de datos¶
En esta sección aprenderás cómo acceder, modificar y extraer valores de un arreglo o matriz utilizando índices. Este proceso se conoce como indexado (indexing) y es esencial para trabajar con subconjuntos de datos.
NumPy sigue una convención de índices basada en 0, lo que significa que el primer elemento está en la posición 0, no en 1.
🔢 Acceder a elementos en arreglos¶
Creamos un arreglo unidimensional (vector) con 4 elementos
a = np.array([10, 20, 30, 40]) Accedemos al primer elemento del arreglo (índice 0)
print("Primer elemento:", a[0])Primer elemento: 10
Accedemos al último elemento usando índice negativo (-1). En NumPy, los índices negativos cuentan desde el final hacia el principio
print("Último elemento:", a[-1]) # índice negativoÚltimo elemento: 40
Accedemos a un rango de elementos del índice 1 al 2 (el índice 3 no se incluye)
print("Rango del índice 1 al 2:", a[1:3]) # → [20 30]Rango del índice 1 al 2: [20 30]
Modificamos el valor en la posición 2 (índice 2)
a[2] = 100
print("Nuevo arreglo:", a) # → [10 20 100 40]Nuevo arreglo: [ 10 20 100 40]
🧊 Acceso y modificación en matrices (2D arrays)¶
Los arreglos bidimensionales —también llamados matrices— se indexan usando la notación [fila, columna]. NumPy empieza a contar desde 0.
Creamos una matriz 3x3 con valores del 0 al 8
matriz = np.arange(9).reshape(3, 3)
print("Matriz original:\n", matriz)Matriz original:
[[0 1 2]
[3 4 5]
[6 7 8]]
🎯 Acceder a un solo valor¶
Elemento en la fila 0, columna 2
print("Elemento [0, 2]:", matriz[0, 2]) # → 2Elemento [0, 2]: 2
Último elemento usando índices negativos
print("Último elemento:", matriz[-1, -1]) # → 8Último elemento: 8
🔍 Seleccionar una fila o columna completa¶
Fila completa (por ejemplo, la fila 1)
print("Fila 1:", matriz[1, :]) # → [3 4 5]Fila 1: [3 4 5]
Columna completa (por ejemplo, la columna 0)
print("Columna 0:", matriz[:, 0]) # → [0 3 6]Columna 0: [0 3 6]
✏️ Modificar un valor¶
Cambiar el valor en la posición [2, 2]
matriz[2, 2] = 99
print("Matriz modificada:\n", matriz)Matriz modificada:
[[ 0 1 2]
[ 3 4 5]
[ 6 7 99]]
✅ En resumen¶
Podemos seleccionar fácilmente subconjuntos de datos dentro de nuestros objetos numpy.ndarray usando índices, slicing, o rangos. Estas herramientas son esenciales para analizar, filtrar y transformar datos en cualquier proyecto científico.
📸 La siguiente imagen (extraída de Scipy Lectures) muestra gráficamente cómo funciona el indexado en NumPy:
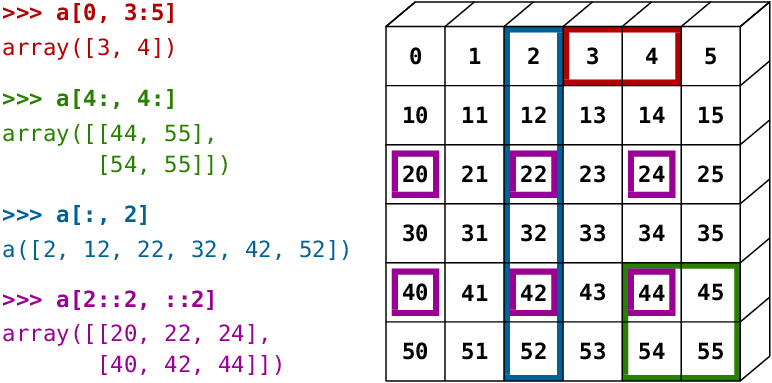
Figure 1:Indexing in NumPy — from Scipy Lectures
🏋️ Práctica: Indexación¶
Dada esta matriz de precipitación (mm) de 3 estaciones durante 4 días:
precip = np.array([[12, 5, 0, 18],
[8, 15, 22, 10],
[0, 3, 8, 12]])Realiza las siguientes tareas:
Extrae la precipitación del día 3 en todas las estaciones (tercera columna)
Extrae todos los valores de la estación 2 (segunda fila)
Cambia el valor del día 1, estación 1 a 15 mm
¿Cuál fue el día con mayor precipitación promedio?
5. Estadísticas y funciones comunes en arreglos¶
En esta sección aprenderás a aplicar funciones estadísticas básicas como suma, promedio y desviación estándar sobre arreglos (arrays) en NumPy. Estas funciones son fundamentales para analizar y resumir datos numéricos.
📊 Operaciones estadísticas en 1D¶
NumPy incluye métodos integrados que permiten calcular estadísticas comunes de forma rápida y directa. A continuación, creamos un arreglo unidimensional y aplicamos operaciones estadísticas básicas:
a = np.array([1, 2, 3, 4, 5])Calculamos la suma total de los elementos del arreglo
# Calculamos la suma total de los elementos del arreglo
print("Suma:", np.sum(a)) # 15
# Calculamos el valor promedio (media aritmética)
print("Promedio (mean):", np.mean(a)) # 3.0
# Calculamos la desviación estándar, que mide la dispersión de los datos
print("Desviación estándar (std):", np.std(a)) # 1.414...
# Obtenemos el valor mínimo del arreglo
print("Mínimo:", np.min(a)) # 1
# Obtenemos el valor máximo del arreglo
print("Máximo:", np.max(a)) Suma: 15
Promedio (mean): 3.0
Desviación estándar (std): 1.4142135623730951
Mínimo: 1
Máximo: 5
🧮 Estadísticas en arreglos multidimensionales¶
En esta parte aplicamos funciones estadísticas en arreglos 2D. Podemos especificar el eje (axis) para que la operación se aplique por filas o columnas.
Creamos una matriz de 2 filas por 3 columnas
matriz = np.array([[1, 2, 3],
[4, 5, 6]])# Suma total de todos los elementos
print("Suma total:", np.sum(matriz)) # → 21
# Suma por filas: suma horizontal (uno por cada fila)
print("Suma por filas (axis=1):", np.sum(matriz, axis=1)) # → [6 15]
# Promedio por columnas: promedio vertical para cada columna
print("Promedio por columnas (axis=0):", np.mean(matriz, axis=0)) # → [2.5 3.5 4.5]Suma total: 21
Suma por filas (axis=1): [ 6 15]
Promedio por columnas (axis=0): [2.5 3.5 4.5]
📊 Entendiendo el parámetro axis¶
Al trabajar con matrices 2D, podemos aplicar funciones en diferentes direcciones:
axis=0: Operación vertical ↓ → colapsa filas (resultado: una fila con valores por columna)axis=1: Operación horizontal → → colapsa columnas (resultado: una columna con valores por fila)
Ejemplo visual:
Matriz original: axis=0 (↓) axis=1 (→)
[[1, 2, 3], → [4, 6, 8] → [6, 12, 18]
[3, 4, 5]] suma por col. suma por filaPiensa en axis=0 como “colapsar verticalmente” y axis=1 como “colapsar horizontalmente”.
axis=0 → operación vertical (por columnas)
axis=1 → operación horizontal (por filas)
📈 Otras funciones útiles¶
Estas funciones adicionales permiten obtener estadísticas acumulativas y centralizadas, ideales para análisis más detallados.
a = np.array([1, 3, 5, 7, 9])# Calcula la mediana (valor central) del arreglo
print("Mediana:", np.median(a)) # → 5
# Calcula la desviación estándar
print("Desviación estándar:", np.std(a)) # → 2.828...
# Suma acumulada: suma progresiva de los elementos
print("Valor acumulado:", np.cumsum(a)) # → [1 4 9 16 25]
# Producto acumulado: multiplicación progresiva de los elementos
print("Producto acumulado:", np.cumprod(a)) # → [1 3 15 105 945]Mediana: 5.0
Desviación estándar: 2.8284271247461903
Valor acumulado: [ 1 4 9 16 25]
Producto acumulado: [ 1 3 15 105 945]
Estas funciones son fundamentales para describir la estructura estadística de tus datos de manera sencilla y rápida.
🏋️ Práctica: Estadísticas¶
Dado un arreglo de temperaturas diarias de Bogotá durante 10 días:
temps = np.array([22, 24, 23, 26, 25, 21, 20, 22, 24, 23])Calcula lo siguiente:
Temperatura promedio del período
Temperatura máxima y mínima
Desviación estándar de las temperaturas
¿Cuántos días tuvieron temperatura mayor a 23°C? (pista: usa boolean indexing con
temps > 23)
6. 🛰️ Broadcasting en NumPy¶
En esta sección conocerás uno de los conceptos más potentes (y confusos al principio) de NumPy: el broadcasting.
Este mecanismo permite realizar operaciones entre arreglos de formas distintas, sin necesidad de copiar o redimensionar los datos manualmente.
🧠 Analogía: ¿Qué es broadcasting?¶
Piensa en broadcasting como “copiar y pegar automático”:
Si sumas un número a una matriz, NumPy “copia” ese número para cada elemento
Si sumas una fila a una matriz, NumPy “copia” esa fila para cada fila de la matriz
Es como usar “rellenar hacia abajo” en Excel, pero automático y eficiente
Visualización:
Caso 1: Escalar + Matriz
5 + [[1, 2, 3], → [[6, 7, 8],
[4, 5, 6]] [9, 10, 11]]
(el 5 se "copia" a cada posición)
Caso 2: Vector + Matriz
[1, 2, 3] + [[10, 20, 30], → [[11, 22, 33],
[40, 50, 60]] [41, 52, 63]]
(el vector se "copia" para cada fila)Broadcasting funciona cuando las dimensiones son compatibles. NumPy ajusta automáticamente las formas cuando es posible.
❓ ¿Qué es el broadcasting?¶
Broadcasting es una regla que aplica NumPy cuando se realizan operaciones entre arreglos que no tienen la misma forma (shape).
Si una de las dimensiones es 1 o puede “extenderse” a la forma del otro arreglo, NumPy lo ajusta automáticamente.
Esto permite, por ejemplo, sumar una fila a cada fila de una matriz, sin necesidad de usar un bucle
for.
📐 Ejemplo 1: sumar un escalar a un arreglo¶
a = np.array([10, 20, 30])print("Original:", a)Original: [10 20 30]
Sumamos un escalar (3) a todos los elementos del arreglo
print("Suma con escalar:", a + 3)Suma con escalar: [13 23 33]
✅ NumPy aplica el escalar a cada elemento del arreglo —no se necesita un bucle.
🧱 Ejemplo 2: sumar una fila a una matriz¶
Definimos dos matrices:
matriz = np.array([[1, 2, 3],
[4, 5, 6]])
fila = np.array([10, 20, 30])matriz, fila(array([[1, 2, 3],
[4, 5, 6]]),
array([10, 20, 30]))Suma fila a cada fila de la matriz
resultado = matriz + fila
print("Resultado:\n", resultado)Resultado:
[[11 22 33]
[14 25 36]]
✅ Aquí fila tiene forma (3,) y se extiende a (2, 3) para coincidir con matriz.
⚠️ ¿Cuándo no funciona el broadcasting?¶
El broadcasting solo funciona si las dimensiones finales coinciden o si una de ellas es 1. De lo contrario, obtendrás un error:
a = np.array([1, 2, 3]) # shape: (3,)
b = np.array([[1, 2], # shape: (2, 2)
[3, 4]])a.shape, b.shape((3,), (2, 2))Esto genera un error de broadcasting porque las formas no son compatibles
# Ejemplo de error por formas incompatibles
a = np.array([1, 2, 3])
b = np.array([[10, 20]])
print("Forma de a:", a.shape)
print("Forma de b:", b.shape)
try:
result = a + b
except ValueError as e:
print(f"\n❌ Error de broadcasting: {e}")Forma de a: (3,)
Forma de b: (1, 2)
❌ Error de broadcasting: operands could not be broadcast together with shapes (3,) (1,2)
7. 🧰 Otras herramientas útiles de NumPy¶
En esta sección exploramos algunas funciones adicionales muy útiles para la manipulación de datos:
📐 cambio de forma (reshape),
📎 combinación de arreglos (concatenate), y
🔍 filtrado condicional (boolean indexing).
📐 Cambio de forma (reshape)¶
Podemos reorganizar los datos de un arreglo sin cambiar su contenido:
a = np.arange(12)
print("Original:", a)Original: [ 0 1 2 3 4 5 6 7 8 9 10 11]
Cambiamos la forma a una matriz de 3 filas x 4 columnas
a_reshaped = a.reshape((3, 4))
print("Reshape (3x4):\n", a_reshaped)Reshape (3x4):
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
⚠️ El número total de elementos debe mantenerse igual.
📎 Concatenación y apilamiento¶
NumPy nos permite unir varios arreglos en una sola estructura:
a = np.array([[1, 2],
[3, 4]])
b = np.array([[5, 6]])Apilamos verticalmente (una fila debajo de la otra)
print("Vertical (vstack):\n", np.vstack((a, b)))Vertical (vstack):
[[1 2]
[3 4]
[5 6]]
Apilamos horizontalmente (una columna al lado de la otra)
print("Horizontal (hstack):\n", np.hstack((a, a)))Horizontal (hstack):
[[1 2 1 2]
[3 4 3 4]]
🔍 Filtrado con máscaras booleanas¶
Podemos seleccionar elementos de un arreglo que cumplan una condición:
a = np.array([10, 20, 30, 40, 50])Creamos una máscara booleana
mask = a > 30
print("Máscara:", mask)Máscara: [False False False True True]
Aplicamos la máscara para filtrar valores
print("Valores mayores a 30:", a[mask])Valores mayores a 30: [40 50]
Este método es muy potente para extraer datos que cumplen ciertos criterios sin bucles explícitos.
✅ Conclusión¶
En este cuadernillo aprendiste los fundamentos del trabajo con NumPy, una herramienta esencial para el procesamiento numérico y científico con Python.
🔑 En resumen:
Comprendiste qué es un
arrayy cómo crearlo.Realizaste operaciones matemáticas básicas y estadísticas.
Aplicaste técnicas de indexación y slicing.
Exploraste el concepto de broadcasting para operaciones entre formas diferentes.
Conociste herramientas adicionales como
reshape,concatenatey filtrado condicional.
Estas habilidades serán la base para trabajar con librerías más avanzadas como Pandas y Xarray.
🔗 Recursos recomendados¶
¡Buen trabajo! 💪 Ahora estás listo para continuar con Pandas y avanzar hacia el análisis de datos tabulares y series de tiempo.
✅ Auto-evaluación¶
Al finalizar este cuadernillo deberías poder:
Crear arreglos 1D y 2D usando diferentes métodos (
np.array,np.arange,np.linspace,np.zeros,np.ones)Aplicar operaciones matemáticas elemento a elemento
Indexar y modificar valores en arreglos usando índices y slices
Calcular estadísticas básicas (suma, promedio, desviación estándar, máximo, mínimo)
Explicar qué es broadcasting y cuándo se aplica automáticamente
Usar boolean indexing para filtrar datos
Trabajar con el parámetro
axisen funciones de agregaciónCombinar reshape, concatenación y otras operaciones útiles
Si puedes hacer todo esto, ¡estás listo para Pandas y Xarray! 🎉
Fuentes y Referencias¶
Rose, B. E. J., Kent, J., Tyle, K., Clyne, J., Banihirwe, A., Camron, D., May, R., Grover, M., Ford, R. R., Paul, K., Morley, J., Eroglu, O., Kailyn, L., & Zacharias, A. (2023). Pythia Foundations (Version v2023.05.01) Rose et al. (2023)
- Rose, B., Kent, J., Tyle, K., Clyne, Banihirwe, A., Camron, D., Ford, R., Morley, J., Grover, M., Eroglu, O., Paul, K., May, R., Lkailynncar, Irving, D., Uieda, L., Ojaybee, Blain, P., & Moon, Z. (2023). ProjectPythia/pythia-foundations: v2023.05.01. Zenodo. 10.5281/ZENODO.7884572