HoloViz Visualization
Overview
The ability to dynamically render, pan, zoom, animate and perform other dynamic operations on data can provide many benefits, such as providing greater data fidelity within the same plot. HoloViz provides high-level tools (such as Holoviews, Datashader, Geoviews, etc.) to visualize even the very large datasets efficiently.
This notebook explores interactively plotting using an unstructured grid dataset in the MPAS format with Holoviews, Datashader, and Geoviews.
Attention
If you are in this notebook to actually learn about and/or visualize unstructured grids, we highly recommend checking out the UXarray Cookbook that is a comprehensive showcase of workflows & techniques for visualizing Unstructured Grids using UXarray. UXarray is a Python package that:
Provides Xarray-styled functionality for working with unstructured grids built around the UGRID conventions
Supports not only MPAS but also several other formats such as UGRID, SCRIP, and Exodus
Enables significant data analysis and visualization functionality for unstructured grid research, which makes working with unstructured grids a breeze
e.g. UXarray internally handles majority of the utility functions and data preparation steps mentioned throughout this notebook and provides user with convenient visualization and analysis functions
This notebook demonstrates:
Use of HoloViz tools for interactive plotting
Different interactivity schemes
Use of the MPAS format’s connectivity information to render data on the native grid (hence avoiding costly Delaunay triangulation)
The flow of the content is as follows:
Package imports
MPAS preprocessing for visualization
Utility functions
Data loading
Triangular mesh generation using MPAS’s cell connectivity array from the primal mesh
Interactive Holoviz Plots
Imports
import math as math
import cartopy.crs as ccrs
import dask.dataframe as dd
import geocat.datafiles as gdf # Only for reading-in datasets
import geoviews.feature as gf # Only for displaying coastlines
import holoviews as hv
import numpy as np
import pandas as pd
from holoviews import opts
from holoviews.operation.datashader import rasterize as hds_rasterize
from numba import jit
from xarray import open_mfdataset
n_workers = 1
MPAS Preprocessing
The MPAS data requires some preprocessing to get it ready for visualization such as implementation of a few utility functions, loading the data, and creating triangular mesh out of the data to rasterize.
Utility functions
def unzipMesh(x, tris, t):
"""Splits a global mesh along longitude.
Examine the X coordinates of each triangle in 'tris'. Return an array of 'tris' where
only those triangles with legs whose length is less than 't' are returned.
Parameters
----------
x: numpy.ndarray
x-coordinates of each triangle in 'tris'
tris: numpy.ndarray
Triangle indices for each vertex in the MPAS file, in counter-clockwise order
t: float
Threshold value
"""
return tris[
(np.abs((x[tris[:, 0]]) - (x[tris[:, 1]])) < t)
& (np.abs((x[tris[:, 0]]) - (x[tris[:, 2]])) < t)
]
def triArea(x, y, tris):
"""Computes the signed area of a triangle.
Parameters
----------
x: numpy.ndarray
x-coordinates of each triangle in 'tris'
y: numpy.ndarray
y-coordinates of each triangle in 'tris'
tris: numpy.ndarray
Triangle indices for each vertex in the MPAS file
"""
return ((x[tris[:, 1]] - x[tris[:, 0]]) * (y[tris[:, 2]] - y[tris[:, 0]])) - (
(x[tris[:, 2]] - x[tris[:, 0]]) * (y[tris[:, 1]] - y[tris[:, 0]])
)
def orderCCW(x, y, tris):
"""Reorder triangles as necessary so they all have counter clockwise winding order.
CCW is what Datashader and MPL require.
Parameters
----------
x: numpy.ndarray
x-coordinates of each triangle in 'tris'
y: numpy.ndarray
y-coordinates of each triangle in 'tris'
tris: numpy.ndarray
Triangle indices for each vertex in the MPAS file
"""
tris[triArea(x, y, tris) < 0.0, :] = tris[triArea(x, y, tris) < 0.0, ::-1]
return tris
def createHVTriMesh(x, y, triangle_indices, var, n_workers=1):
"""Create a Holoviews Triangle Mesh suitable for rendering with Datashader
This function returns a Holoviews TriMesh that is created from a list of coordinates, 'x'
and 'y', an array of triangle indices that addresses the coordinates in 'x' and 'y', and
a data variable 'var'. The data variable's values will annotate the triangle vertices
Parameters
----------
x: numpy.ndarray
Projected x-coordinates of each triangle in 'tris'
y: numpy.ndarray
Projected y-coordinates of each triangle in 'tris'
triangle_indices: numpy.ndarray
Triangle indices for each vertex in the MPAS file, in counter-clockwise order
var: numpy.ndarray
Data variable from which the triangle vertex values are read.
n_workers: int
Number of workers, for Dask
"""
# Declare verts array
verts = np.column_stack([x, y, var])
# Convert to pandas
verts_df = pd.DataFrame(verts, columns=["x", "y", "z"])
tris_df = pd.DataFrame(triangle_indices, columns=["v0", "v1", "v2"])
# Convert to dask
verts_ddf = dd.from_pandas(verts_df, npartitions=n_workers)
tris_ddf = dd.from_pandas(tris_df, npartitions=n_workers)
# Declare HoloViews element
tri_nodes = hv.Nodes(verts_ddf, ["x", "y", "index"], ["z"])
trimesh = hv.TriMesh((tris_ddf, tri_nodes))
return trimesh
@jit(nopython=True)
def triangulatePoly(verticesOnCell, nEdgesOnCell):
"""Triangulate MPAS dual mesh:
Triangulate each polygon in a heterogenous mesh of n-gons by connecting
each internal polygon vertex to the first vertex. Uses the MPAS
auxilliary variables verticesOnCell, and nEdgesOnCell.
The function is decorated with Numba's just-in-time compiler so that it is translated into
optimized machine code for better peformance
Parameters
----------
verticesOnCell: numpy.ndarray
Connectivity array that stores the vertex indices that surround a given cell
nEdgesOnCell: numpy.ndarray
Number of edges on a given cell.
"""
# Calculate the number of triangles. nEdgesOnCell gives the number of vertices for each cell (polygon)
# The number of triangles per polygon is the number of vertices minus 2.
nTriangles = np.sum(nEdgesOnCell - 2)
triangles = np.ones((nTriangles, 3), dtype=np.int64)
nCells = verticesOnCell.shape[0]
triIndex = 0
for j in range(nCells):
for i in range(nEdgesOnCell[j] - 2):
triangles[triIndex][0] = verticesOnCell[j][0]
triangles[triIndex][1] = verticesOnCell[j][i + 1]
triangles[triIndex][2] = verticesOnCell[j][i + 2]
triIndex += 1
return triangles
Load data and coordinates
Currently, the 30-km resolution dataset is used in this example and is available at geocat-datafiles. However, the other resolutions of these data are stored on NCAR’s Glade data storage because of their size. Due to their size, the higher resolution data sets are only distributed with two variables in them:
relhum_200hPa: Relative humidity vertically interpolated to 200 hPa
vorticity_200hPa: Relative vorticity vertically interpolated to 200 hPa
The “relhum_200hPa” variable is computed on the MPAS ‘primal’ mesh, while “vorticity_200hPa” is computed on the MPAS ‘dual’ mesh.
# Load data
datafiles = (
gdf.get(
"netcdf_files/MPAS/FalkoJudt/dyamond_1/30km/diag.2016-08-20_00.00.00_subset.nc"
),
gdf.get("netcdf_files/MPAS/FalkoJudt/dyamond_1/30km/x1.655362.grid_subset.nc"),
)
primalVarName = "relhum_200hPa"
dualVarName = "vorticity_200hPa"
central_longitude = 0.0
ds = open_mfdataset(datafiles, decode_times=False)
primalVar = ds[primalVarName].isel(Time=0).values
dualVar = ds[dualVarName].isel(Time=0).values
# Fetch lat and lon coordinates for the primal and dual mesh.
lonCell = ds["lonCell"].values * 180.0 / math.pi
latCell = ds["latCell"].values * 180.0 / math.pi
lonCell = ((lonCell - 180.0) % 360.0) - 180.0
lonVertex = ds["lonVertex"].values * 180.0 / math.pi
latVertex = ds["latVertex"].values * 180.0 / math.pi
lonVertex = ((lonVertex - 180.0) % 360.0) - 180.0
Downloading file 'netcdf_files/MPAS/FalkoJudt/dyamond_1/30km/diag.2016-08-20_00.00.00_subset.nc' from 'https://github.com/NCAR/GeoCAT-datafiles/raw/main/netcdf_files/MPAS/FalkoJudt/dyamond_1/30km/diag.2016-08-20_00.00.00_subset.nc' to '/home/runner/.cache/geocat'.
Downloading file 'netcdf_files/MPAS/FalkoJudt/dyamond_1/30km/x1.655362.grid_subset.nc' from 'https://github.com/NCAR/GeoCAT-datafiles/raw/main/netcdf_files/MPAS/FalkoJudt/dyamond_1/30km/x1.655362.grid_subset.nc' to '/home/runner/.cache/geocat'.
Generate triangular mesh using MPAS connectivity information
Primal mesh
In this example, we use the MPAS cellsOnVertex auxilliary variable, which defines mesh connectivity for the MPAS grid. Specifically, this variable tells us the cell indices contained by each cell.
Important
The benefits of this are twofold:
We’re using the actual mesh description from the MPAS output file
For large grid this is much faster than synthesizing the connectivity information (e.g. by triangulating them with, for example, Delaunay triangulation).
So, first let’s:
Get the triangle indices (i.e. MPAS connectivity),
Make sure it is all in counter-clockwise order,
“Unzip” the mesh along the longitude (for now, assuming the central longitude from the map projection is 0.0, i.e. cutting the mesh where longitude wraps around from -180.0 to 180.0)
Project vertices from geographic to PCS coordinates
Create Holoviews TriMesh
Note
Indexing in MPAS starts from 1, not zero :-(
tris = ds.cellsOnVertex.values - 1
tris = orderCCW(lonCell, latCell, tris)
tris = unzipMesh(lonCell, tris, 90.0)
projection = ccrs.Robinson(central_longitude=central_longitude)
xPCS, yPCS, _ = projection.transform_points(ccrs.PlateCarree(), lonCell, latCell).T
trimesh = createHVTriMesh(xPCS, yPCS, tris, primalVar, n_workers=n_workers)
Dual mesh
In this example though, we use the MPAS verticesOnCell and nEdgesOnCell auxilliary variables, which defines mesh connectivity for the MPAS dual grid. A lot of details in the following code is similarv to those in the primal mesh’s case except triangulatePoly() wheere we decompose each cell into triangles since for the dual mesh, the data are located on triangle centers, which correspond to cell (polygon) vertices.
verticesOnCell = ds.verticesOnCell.values - 1
nEdgesOnCell = ds.nEdgesOnCell.values
tris_dual = triangulatePoly(verticesOnCell, nEdgesOnCell)
tris_dual = unzipMesh(lonVertex, tris_dual, 90.0)
projection = ccrs.Robinson(central_longitude=central_longitude)
xPCS_dual, yPCS_dual, _ = projection.transform_points(
ccrs.PlateCarree(), lonVertex, latVertex
).T
trimesh_dual = createHVTriMesh(
xPCS_dual, yPCS_dual, tris_dual, dualVar, n_workers=n_workers
)
Interactive HoloViz Plots
Note
Since the emphasis of these plots is the interactivity, we will not provide much detail on the features/arguments other than interactivity-related ones, but such details to some extent can still be found in the code comments.
HoloViz tools provide essential interactivity features such as panning, zooming, hovering, clickable/selectable legends, etc. on a plot.
Note
The first step to achieve interactivity with HoloViz tools is to choose bokeh as
the backend:
hv.extension("bokeh")
Let’s define keyword arguments that will be commonly used for all of the plots and their opts throughout. For that, the plotting arguments are aggregator=mean to use the average of node values for shading in the rasterization and precompute=True to cache the data internally; the opts arguments are nothing more than opting in to showing the colorbar and using a colormap called “coolwarm”:
plot_kwargs = {
"aggregator": "mean",
"precompute": True,
}
opts_kwargs = {
"colorbar": True,
"cmap": "coolwarm",
}
Holoviews’ options system: opts
HoloViz packages provide high-level visualization functions that allow the customization of plot features through optional arguments. Furthermore, the HoloViews options system allows customizing a plot from title to size, legend, axes, and more. This system works by calling the .opts() method through a HoloViews plot object. We will set the opts defaults below and then customize plots throughout the notebook via .opts(). Keep an eye on them!
opts.defaults(
opts.Image(frame_width=600, data_aspect=1),
)
Pan & zoom
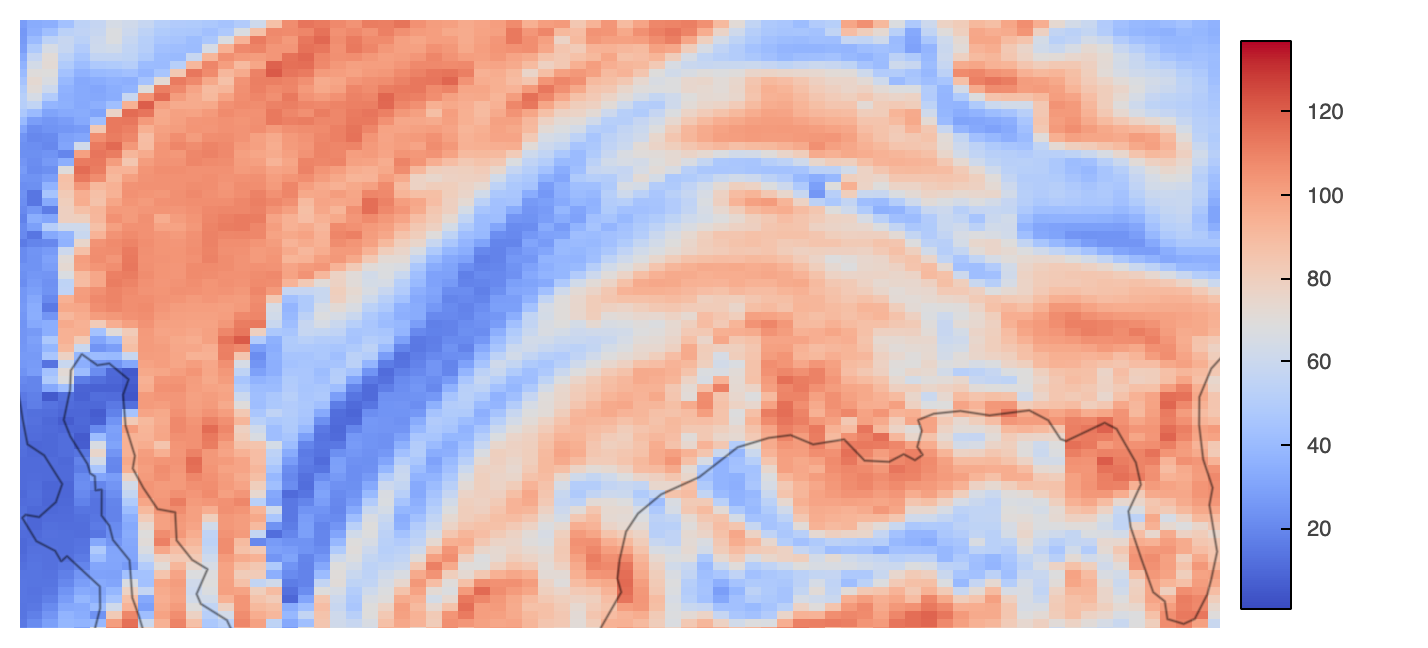
Bokeh-rendered HoloViz plots come with default pan and zoom (box & wheel), tools as well as save and reset options in the very right. Just look at the following plot for those features, which uses Datashader’s rasterization method to visualize the data.
rasterized = hds_rasterize(trimesh, **plot_kwargs)
rasterized.opts(**opts_kwargs) * gf.coastline(projection=projection)
Hover
Use tools=['hover'] can be used to get the plot to display data values while hovering over the plot (there are other tools that can be selected, too, but those will not be covered in this notebook). See the below plot (let’s use the dual mesh data this time just for the sake of assortment of visualizations) and hover you cursor over it:
rasterized = hds_rasterize(trimesh_dual, **plot_kwargs)
rasterized.opts(tools=["hover"], clim=(-4e-4, 4e-4), **opts_kwargs) * gf.coastline(
projection=projection
)
Dynamic plot
You can decide whether to return a dynamic plot that sends updates on widget and zoom/pan
events or whether all the data should be embedded by using the boolean dynamic argument.
The default value of this argument is True, so all the previously rendered plots were
already dynamic.
Warning
If you are looking at this through the Pythia Cookbook gallery webpage (i.e. this is a rendered notebook as html), you cannot experience how the “dynamic” option works. To do that, you have to execute the notebook live (e.g. through the Binder link we provide for the cookbook or by executing it in your local).
Now let’s look at a non-dynamic plot (i.e. dynamic=False):
rasterized = hds_rasterize(trimesh, **plot_kwargs, dynamic=False)
rasterized.opts(**opts_kwargs) * gf.coastline(projection=projection)
Tip
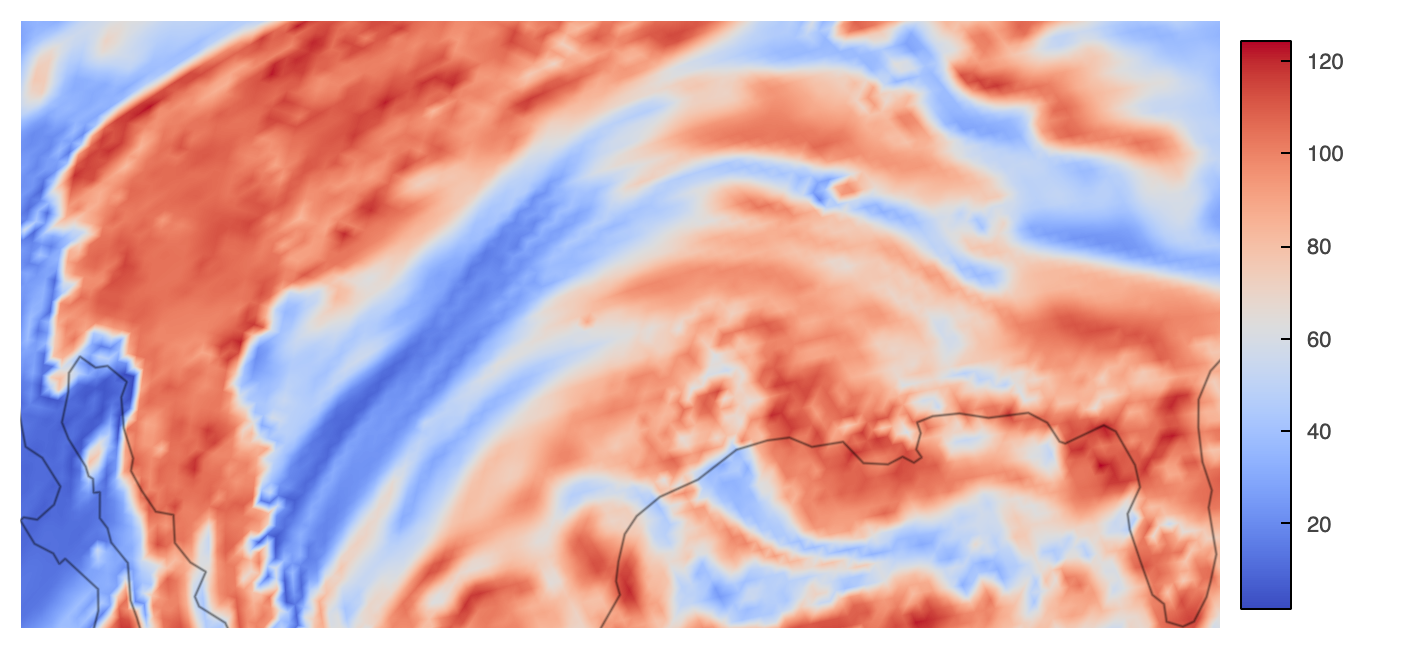
This plot does not look immediately different than the prior ones where dynamic=True, right? Yes, in the global view, but try zooming into the plot (again, if you are executing notebook rather than looking at the rendered one), and see how dynamic vs. non-dynamic plots look like. See the below comparison for instance:
Non-Dynamic-Zoomed |
Dynamic-Zoomed |
|---|---|
|
|
Summary
HoloViz technologies can be used in order to create interactive plots when Bokeh is used as the backend. Even though a really large dataset (e.g. km-scale) is not showcased in this notebook, HoloViz packages are reasonably performant with visualization of such data, too.
Resources and references
MPAS Mesh Specification for those interested