Skip to article frontmatterSkip to article content
Site not loading correctly?

This may be due to an incorrect BASE_URL configuration. See the MyST Documentation for reference.

Feedback analysis using radiative kernels

Project Pythia Logo

Overview

This notebook details the steps required to perform a radiative kernel analysis.

Prerequisites

ConceptsImportanceNotes
Loading CMIP6 data with Intake-ESMHelpful
Intro to XarrayNecessary

  • Time to learn: 60 minutes

Imports

import xarray as xr
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import CenteredNorm
import cartopy.crs as ccrs
import xesmf as xe
import intake
import s3fs
import fsspec
import glob

Loading in required data

Climate model output

In this example, we will perform the analysis on a single model from the CMIP6 ensemble, CESM2. The simplest way to calculate feedbacks is to take differences between two climate states, as opposed to regressions. Here we use runs with:

  • preindustrial conditions (piControl) as the control climate

  • instantaneously quadrupled CO2_2 (abrupt-4xCO2) as the perturbed climate

We will use CMIP6 data hosted on Pangeo’s Google Cloud Storage:

cat_url = 'https://storage.googleapis.com/cmip6/pangeo-cmip6.json'
col = intake.open_esm_datastore(cat_url)

The fields (and CMIP names) required to calculate each feedback are:

  • Albedo: upwelling and downwelling SW radiation at the surface (rsus and rsds)

  • Temperature (Planck and lapse rate): air temperature (ta) and surface temperature (ts)

  • Water vapor: specific humidity (hus) and air temperature

  • SW CRE: Net SW radiation at TOA (down rsdt minus up rsut) and clear-sky versions (down, which is the same, minus up rsutcs)

  • LW CRE: Net LW radiation at TOA (rlut) and the clear-sky version (rlutcs)

The cloud feedbacks require the results from the other feedbacks to correct for noncloud contributions to the CREs.

We will also need near-surface air temperature (tas) for calculating the change in global mean surface temperature (GMST).

cat = col.search(activity_id='CMIP', experiment_id=['piControl', 'abrupt-4xCO2'], table_id='Amon', source_id='CESM2', 
                 variable_id=['rsus', 'rsds', 'ta', 'ts', 'hus', 'rsdt', 'rsut', 'rsutcs', 'rlut', 'rlutcs', 'tas'])
cat.df
Loading...
dset_dict = cat.to_dataset_dict(zarr_kwargs={'consolidated': True})

--> The keys in the returned dictionary of datasets are constructed as follows:
	'activity_id.institution_id.source_id.experiment_id.table_id.grid_label'
Loading...
Loading...
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "time" starting at index 650. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lat" starting at index 185. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "time" starting at index 679. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lat" starting at index 181. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lon" starting at index 272. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lon" starting at index 278. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "time" starting at index 705. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lat" starting at index 178. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lon" starting at index 267. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "time" starting at index 670. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lat" starting at index 182. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lon" starting at index 274. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "time" starting at index 37. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "plev" starting at index 18. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lat" starting at index 182. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lon" starting at index 273. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "time" starting at index 838. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lat" starting at index 163. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lon" starting at index 245. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "time" starting at index 738. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lat" starting at index 174. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lon" starting at index 261. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "time" starting at index 642. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lat" starting at index 186. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lon" starting at index 280. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "time" starting at index 713. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lat" starting at index 177. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lon" starting at index 265. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "time" starting at index 44. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "plev" starting at index 17. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lat" starting at index 172. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lon" starting at index 258. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "time" starting at index 743. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lat" starting at index 173. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:109: UserWarning: The specified chunks separate the stored chunks along dimension "lon" starting at index 260. This could degrade performance. Instead, consider rechunking after loading.
  ds = xr.open_dataset(url, **xarray_open_kwargs)

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:308: FutureWarning: In a future version of xarray the default value for compat will change from compat='no_conflicts' to compat='override'. This is likely to lead to different results when combining overlapping variables with the same name. To opt in to new defaults and get rid of these warnings now use `set_options(use_new_combine_kwarg_defaults=True) or set compat explicitly.
  self._ds = xr.combine_by_coords(

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:308: FutureWarning: In a future version of xarray the default value for compat will change from compat='no_conflicts' to compat='override'. This is likely to lead to different results when combining overlapping variables with the same name. To opt in to new defaults and get rid of these warnings now use `set_options(use_new_combine_kwarg_defaults=True) or set compat explicitly.
  self._ds = xr.combine_by_coords(

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:308: FutureWarning: In a future version of xarray the default value for compat will change from compat='no_conflicts' to compat='override'. This is likely to lead to different results when combining overlapping variables with the same name. To opt in to new defaults and get rid of these warnings now use `set_options(use_new_combine_kwarg_defaults=True) or set compat explicitly.
  self._ds = xr.combine_by_coords(
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:308: FutureWarning: In a future version of xarray the default value for compat will change from compat='no_conflicts' to compat='override'. This is likely to lead to different results when combining overlapping variables with the same name. To opt in to new defaults and get rid of these warnings now use `set_options(use_new_combine_kwarg_defaults=True) or set compat explicitly.
  self._ds = xr.combine_by_coords(

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:308: FutureWarning: In a future version of xarray the default value for compat will change from compat='no_conflicts' to compat='override'. This is likely to lead to different results when combining overlapping variables with the same name. To opt in to new defaults and get rid of these warnings now use `set_options(use_new_combine_kwarg_defaults=True) or set compat explicitly.
  self._ds = xr.combine_by_coords(

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:308: FutureWarning: In a future version of xarray the default value for compat will change from compat='no_conflicts' to compat='override'. This is likely to lead to different results when combining overlapping variables with the same name. To opt in to new defaults and get rid of these warnings now use `set_options(use_new_combine_kwarg_defaults=True) or set compat explicitly.
  self._ds = xr.combine_by_coords(

ctrl = dset_dict['CMIP.NCAR.CESM2.piControl.Amon.gn']
ctrl
Loading...
pert = dset_dict['CMIP.NCAR.CESM2.abrupt-4xCO2.Amon.gn']
pert
Loading...

Radiative forcing data

To calculate the cloud feedback, we will need the effective radiative forcing (ERF) resulting from 4xCO2, which we can find under another project, RFMIP:

rf_cat = col.search(activity_id='RFMIP', experiment_id='piClim-4xCO2', source_id='CESM2')
rf_cat.df
Loading...
rf_dset_dict = rf_cat.to_dataset_dict(zarr_kwargs={'consolidated': True})

--> The keys in the returned dictionary of datasets are constructed as follows:
	'activity_id.institution_id.source_id.experiment_id.table_id.grid_label'
Loading...
Loading...
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:308: FutureWarning: In a future version of xarray the default value for compat will change from compat='no_conflicts' to compat='override'. This is likely to lead to different results when combining overlapping variables with the same name. To opt in to new defaults and get rid of these warnings now use `set_options(use_new_combine_kwarg_defaults=True) or set compat explicitly.
  self._ds = xr.combine_by_coords(

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:308: FutureWarning: In a future version of xarray the default value for compat will change from compat='no_conflicts' to compat='override'. This is likely to lead to different results when combining overlapping variables with the same name. To opt in to new defaults and get rid of these warnings now use `set_options(use_new_combine_kwarg_defaults=True) or set compat explicitly.
  self._ds = xr.combine_by_coords(

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/intake_esm/source.py:308: FutureWarning: In a future version of xarray the default value for compat will change from compat='no_conflicts' to compat='override'. This is likely to lead to different results when combining overlapping variables with the same name. To opt in to new defaults and get rid of these warnings now use `set_options(use_new_combine_kwarg_defaults=True) or set compat explicitly.
  self._ds = xr.combine_by_coords(

forcing = rf_dset_dict['RFMIP.NCAR.CESM2.piClim-4xCO2.Amon.gn']
forcing
Loading...

Radiative kernels

We will load in radiative kernels from Project Pythia’s storage on JetStream2. We will be using the ERA5 kernels (Huang & Huang 2023).

URL = 'https://js2.jetstream-cloud.org:8001/'
path = f'pythia/ClimKern'
fs = fsspec.filesystem("s3", anon=True, client_kwargs=dict(endpoint_url=URL))
patternKern = f's3://{path}/kernels/ERA5/*.nc'
patternTutorial = f's3://{path}/tutorial_data/*.nc'
filesKern = sorted(fs.glob(patternKern))
filesTutorial = sorted(fs.glob(patternTutorial))
fs.invalidate_cache() # This is necessary to deal with peculiarities of objects served from jetstream2
filesetKern = [fs.open(file) for file in filesKern[0:2]]
filesetTutorial = [fs.open(file) for file in filesKern[0:2]]

We will use the more common TOA kernels.

filesKern
['pythia/ClimKern/kernels/ERA5/SFC_ERA5_Kerns.nc', 'pythia/ClimKern/kernels/ERA5/TOA_ERA5_Kerns.nc']

As we will see in a moment, the naming convention for months as calculated from Xarray’s .groupby() method (“month”, 1-12) is different from what is used in the kernel dataset (“time”, 0-11), so we need to align them:

data_kern = xr.open_dataset(filesetKern[1])
data_kern['time'] = data_kern['time'] + 1
data_kern = data_kern.rename({'time': 'month'})
data_kern
Loading...

Let’s take a look at some of these kernels. First, the albedo kernel, annually averaged:

data_kern.sw_a.mean(dim='month').plot.contourf(levels=20)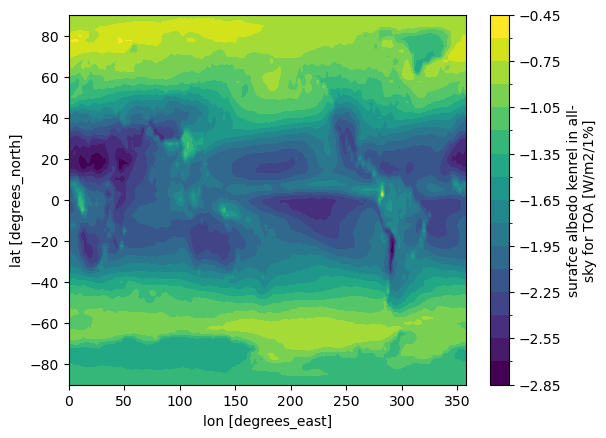
<Figure size 640x480 with 2 Axes>

And the LW water vapor kernel, annually and zonally averaged:

data_kern.lw_q.mean(dim=['month', 'lon']).plot.contourf(levels=40, yincrease=False)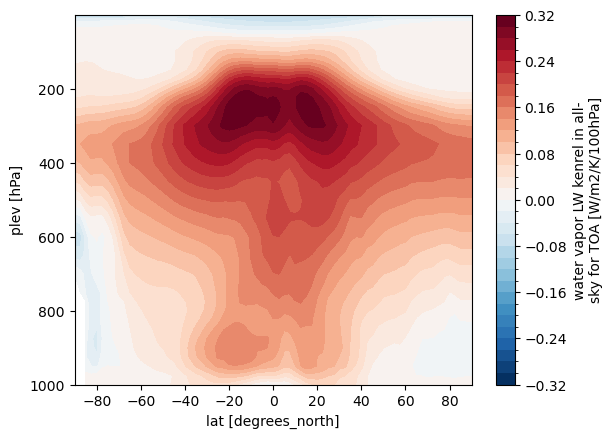
<Figure size 640x480 with 2 Axes>

Preparing data for analysis

Define a function for taking global averages:

def global_average(data):
    weights = np.cos(np.deg2rad(data.lat))
    data_weighted = data.weighted(weights)
    return data_weighted.mean(dim=['lat', 'lon'], skipna=True)

To get a general idea of how the climate changes in these runs, we can plot the 12-month rolling GMST for the two runs:

gmst_ctrl = global_average(ctrl.tas.rolling(time=12, center=True).mean())
gmst_ctrl.sel(time=slice('1150', '1200')).plot()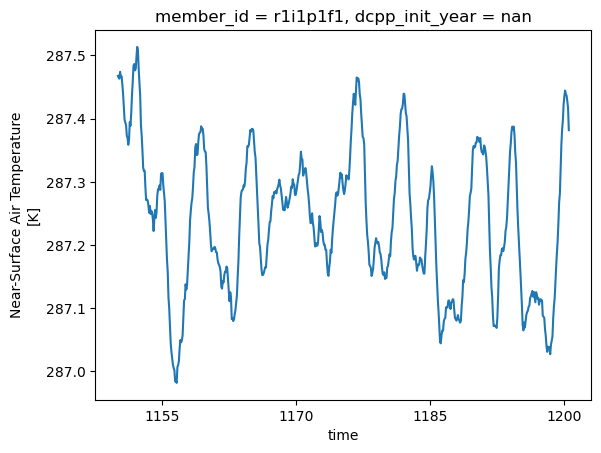
<Figure size 640x480 with 1 Axes>
gmst_pert = global_average(pert.tas.rolling(time=12, center=True).mean())
gmst_pert.sel(time=slice('0949', '0999')).plot()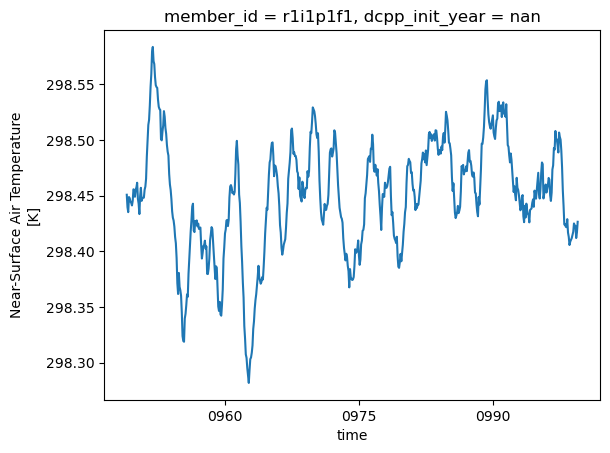
<Figure size 640x480 with 1 Axes>

Calculating the two climate states

Ideally, we would want to compare two equilibrated climates, but since that is usually not possible with standard-length CMIP experiments, we will simply use the monthly climatology over the last 50 years available for each run, which is close enough to equilibrium. The pressure coordinates are in Pa, so let’s convert them to hPa to match the kernels:

ctrl_state = ctrl.sel(time=slice('1150', '1200')).groupby('time.month').mean(dim='time').squeeze()
pert_state = pert.sel(time=slice('0949', '0999')).groupby('time.month').mean(dim='time').squeeze()

ctrl_state['plev'] = ctrl_state['plev']/100
pert_state['plev'] = pert_state['plev']/100
pert_state
Loading...

We will need the change in GMST in order to calculate the feedbacks:

dgmst = global_average(pert_state.tas - ctrl_state.tas).mean(dim='month')
dgmst.load()
Loading...

Regridding

The model output and kernels are not on the same grid, so we will regrid the kernel dataset to the model’s grid using the regridding package xesmf. For reusability, let’s define a function to regrid data:

def regrid(ds_in, regrid_to, method='bilinear'):
    regridder = xe.Regridder(ds_in, regrid_to, method=method, periodic=True, ignore_degenerate=True)
    ds_out = regridder(ds_in)
    return ds_out
regr_kernels = regrid(data_kern, pert_state)
regr_kernels
Loading...

Check that the kernels look as expected:

regr_kernels.sw_a.mean(dim='month').plot.contourf(levels=20)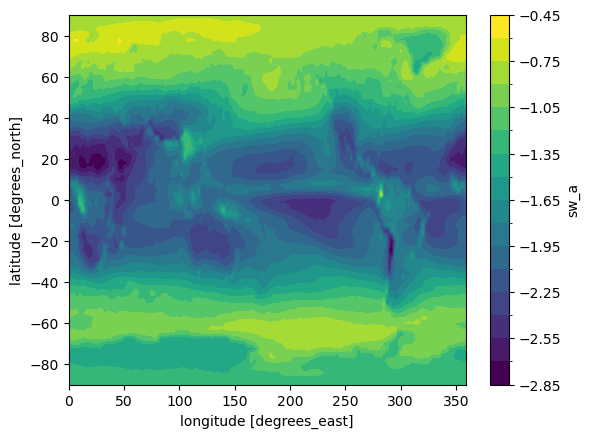
<Figure size 640x480 with 2 Axes>
regr_kernels.lw_q.mean(dim=['month', 'lon']).plot.contourf(levels=40, yincrease=False)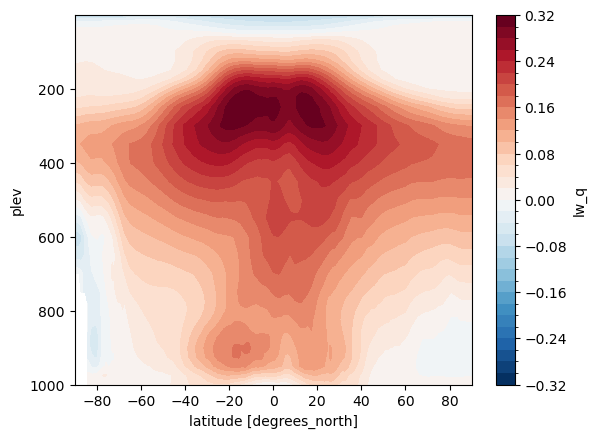
<Figure size 640x480 with 2 Axes>
ctrl_state = ctrl_state.interp_like(regr_kernels, kwargs={"fill_value": "extrapolate"})
pert_state = pert_state.interp_like(regr_kernels, kwargs={"fill_value": "extrapolate"})

Calculating feedbacks

For all noncloud feedbacks, we will calculate both the all-sky and clear-sky (indicated by clr in the kernel dataset here) change in TOA radiation ΔR\Delta R. For the clear-sky calculations, we just use the clear-sky version of the kernel in place of the all-sky kernel. The differences ΔRXclear−ΔRXall\Delta R^\mathrm{clear}_X-\Delta R^\mathrm{all}_X for each feedback XX will be used later to adjust the CREs into proper cloud feedbacks.

For the feedbacks involving fields that are a function of pressure (i.e., temperature and water vapor), we need to mask out the stratosphere. In this notebook, we will approximate this using a function that masks above 100 hPa at the equator and linearly decreases to 300 hPa at the poles:

def tropo_mask(ds):
    return ds.where(ds.plev > ((200/90)*abs(ds.lat) + 100))

Compare:

ctrl_state.ta.mean(dim=['month', 'lon']).plot(yincrease=False)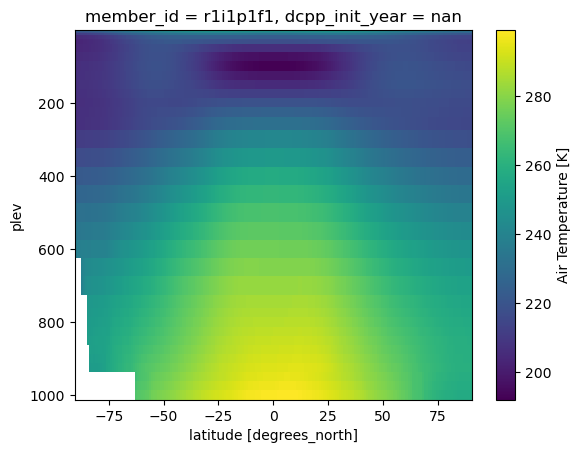
<Figure size 640x480 with 2 Axes>
tropo_mask(ctrl_state.ta.mean(dim=['month', 'lon'])).plot(yincrease=False)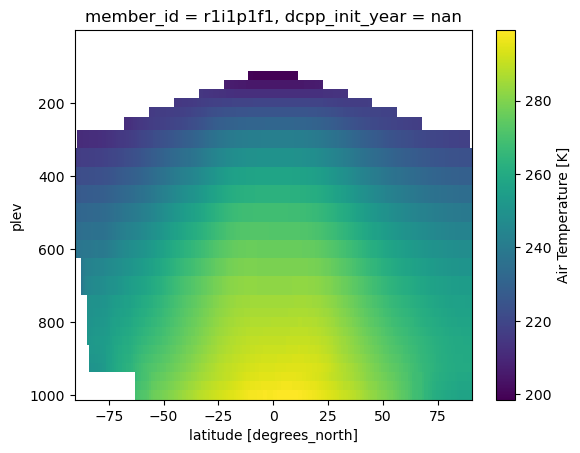
<Figure size 640x480 with 2 Axes>

Surface albedo

The first step is to calculate the change in albedo between the control and perturbed climates. The surface albedo α\alpha is defined as the fraction of downwelling solar radiation at the surface that is reflected back up. That is,

α=Ss↑Ss↓=rsusrsds\alpha=\frac{S^\uparrow_\mathrm{s}}{S^\downarrow_\mathrm{s}}=\frac{\mathtt{rsus}}{\mathtt{rsds}}
(1)
alb_ctrl = (ctrl_state.rsus/ctrl_state.rsds.where(ctrl_state.rsds > 0)).fillna(0)
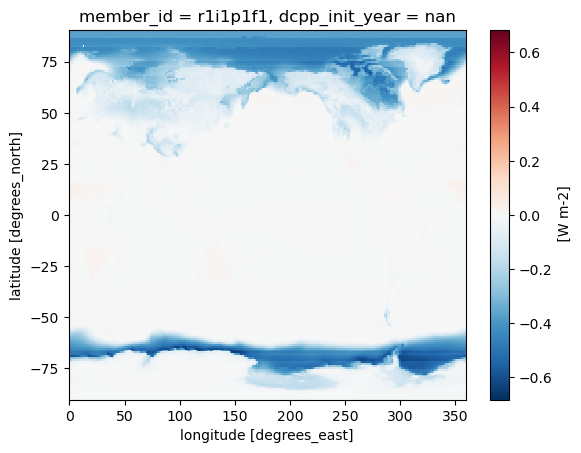
alb_pert = (pert_state.rsus/pert_state.rsds.where(ctrl_state.rsds > 0)).fillna(0)

Note that we avoided dividing by zero by masking regions where rsds = 0 and filling in the resulting nans with 0. Now, take the difference:

dalb = alb_pert - alb_ctrl
dalb.mean(dim='month').plot()
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in divide
  return self.func(*new_argspec)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: divide by zero encountered in divide
  return self.func(*new_argspec)
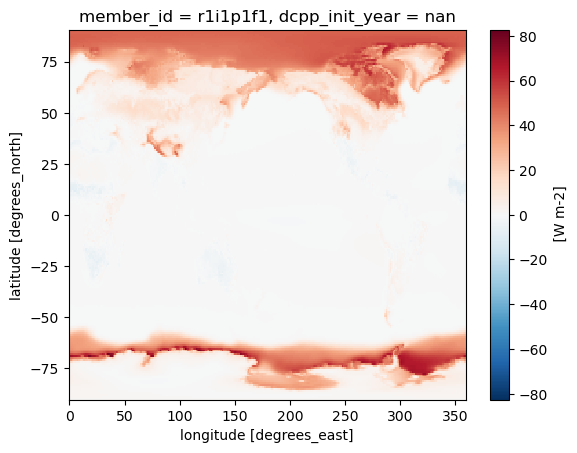
<Figure size 640x480 with 2 Axes>

By multiplying the change in albedo with the albedo kernel, we get the change in TOA radiation (in units W m−2^{-2}) resulting from that change in albedo:

ΔRα=Kα⋅Δα\Delta R_\alpha=K_\alpha\cdot\Delta\alpha
(2)

We also need to multiply by 100 to get albedo as a percentage.

dSW_alb = regr_kernels.sw_a * dalb * 100
dSW_alb = dSW_alb.where(dSW_alb != float('-inf'), np.nan)
dSW_alb_clr = regr_kernels.swclr_a * dalb * 100
dSW_alb_clr = dSW_alb_clr.where(dSW_alb != float('-inf'), np.nan)
dSW_alb.mean(dim='month').plot()
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: divide by zero encountered in divide
  return self.func(*new_argspec)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in divide
  return self.func(*new_argspec)
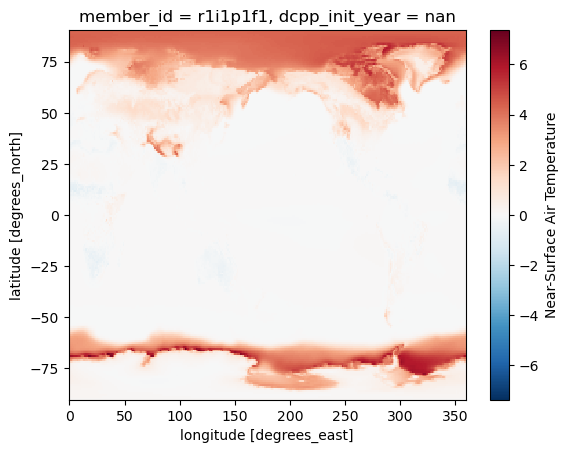
<Figure size 640x480 with 2 Axes>

The feedback in units W m−2^{-2} K−1^{-1} is then calculated by normalizing this change in TOA radiation by the change in GMST:

λα=ΔRαΔTs\lambda_\alpha=\frac{\Delta R_\alpha}{\Delta T_\mathrm{s}}
(3)
alb_feedback = dSW_alb/dgmst
alb_feedback.mean(dim='month').plot()
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in divide
  return self.func(*new_argspec)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: divide by zero encountered in divide
  return self.func(*new_argspec)
<Figure size 640x480 with 2 Axes>

Taking the global and annual average, we get a final value of:

global_average(alb_feedback.mean(dim='month')).load()
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: divide by zero encountered in divide
  return self.func(*new_argspec)
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in divide
  return self.func(*new_argspec)
Loading...

Temperature

The temperature feedback is decomposed into Planck and lapse rate feedbacks, but first, we can calculate the change in TOA LW radiation resulting from changes in surface (ts) and air (ta) temperature. The first step is calculating the changes in surface and air temperature. At the same time, we will interpolate ta to the kernel pressure levels:

dts = pert_state.ts - ctrl_state.ts
dta = pert_state.ta - ctrl_state.ta

Approximate layer thickness:

dp = -dta.plev.diff(dim='plev', label='lower')
dp
Loading...

Then the change in TOA radiation using the kernels:

ΔRTs=KTs⋅ΔTs\Delta R_{T_\mathrm{s}}=K_{T_\mathrm{s}}\cdot\Delta T_\mathrm{s}
(4)

And for feedbacks that involve functions of pressure, we integrate (sum) over the pressure levels. These kernels have units W m−2^{-2} K−1^{-1} (100 hPa)−1^{-1}, so if Δp\Delta p is in hPa,

ΔRT=∑pKT⋅ΔT⋅Δp/100\Delta R_T=\sum_p K_T\cdot\Delta T\cdot\Delta p/100
(5)
dLW_ts = regr_kernels.lw_ts * dts
dLW_ts_clr = regr_kernels.lwclr_ts * dts

dLW_ta = (regr_kernels.lw_t * tropo_mask(dta) * dp/100).sum(dim='plev', skipna=True)
dLW_ta_clr = (regr_kernels.lwclr_t * tropo_mask(dta) * dp/100).sum(dim='plev', skipna=True)
dLW_ts.mean(dim='month').plot()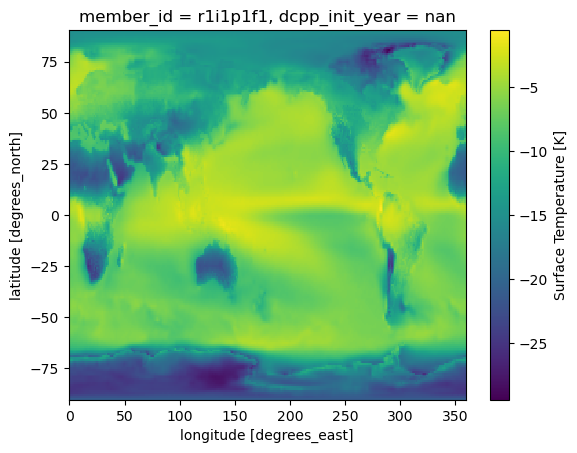
<Figure size 640x480 with 2 Axes>
dLW_ta.mean(dim='month').plot()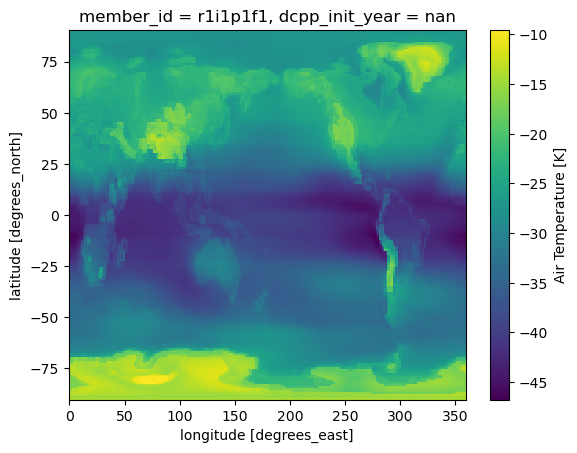
<Figure size 640x480 with 2 Axes>

The full temperature feedback is the sum of these, normalized by the change in GMST:

λT=ΔRTs+ΔRTΔTs\lambda_T=\frac{\Delta R_{T_\mathrm{s}}+\Delta R_T}{\Delta T_\mathrm{s}}
(6)
t_feedback = (dLW_ta + dLW_ts)/dgmst
t_feedback.mean(dim='month').plot(cbar_kwargs={'label': 'W m$^{-2}$ K$^{-1}$'})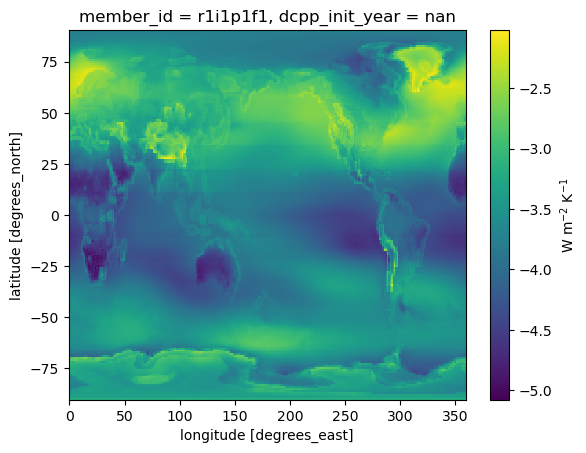
<Figure size 640x480 with 2 Axes>

For the annual and global average, we get in W m−2^{-2} K−1^{-1}:

gm_t_feedback = global_average(t_feedback.mean(dim='month')).load()
gm_t_feedback
Loading...

Planck

There are two components to the Planck feedback:

  1. The change in TOA radiation due to the surface warming (calculated in the previous section)

  2. The change in TOA radiation due to a vertically-uniform warming

We assume a vertically-uniform warming based on the surface temperature. To do this, project the surface warming into the vertical. One way to do this with Xarray is:

dts_3d = dts.expand_dims(dim={'plev': dta.plev})

Check the vertical profile:

dts_3d.mean(dim=['month', 'lon']).plot(yincrease=False)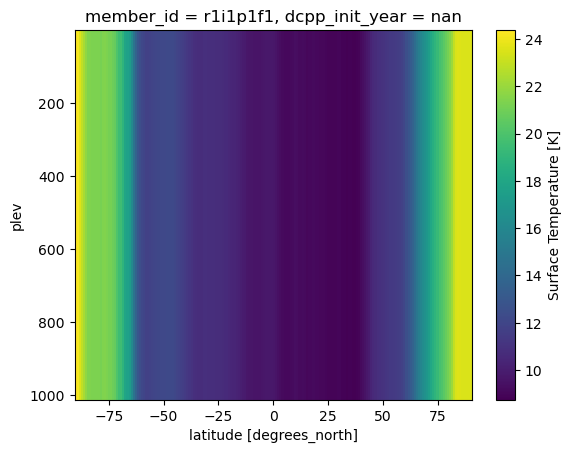
<Figure size 640x480 with 2 Axes>
dLW_dts_3d = (regr_kernels.lw_t * tropo_mask(dts_3d) * dp/100).sum(dim='plev', skipna=True)

The sum of the two components divided by the change in GMST is the Planck feedback:

planck_feedback = (dLW_ts + dLW_dts_3d)/dgmst
planck_feedback.mean(dim='month').plot(cbar_kwargs={'label': 'W m$^{-2}$ K$^{-1}$'})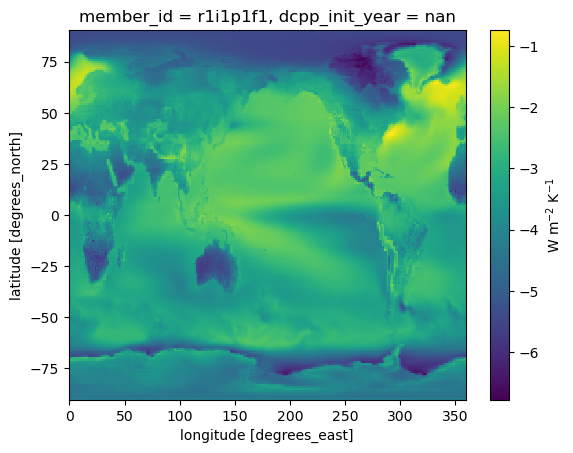
<Figure size 640x480 with 2 Axes>

Annual and global average:

gm_planck_feedback = global_average(planck_feedback.mean(dim='month')).load()
gm_planck_feedback
Loading...

Lapse rate

The lapse rate feedback is calculated using the vertically-nonuniform warming. To do this, we subtract the surface temperature change that we projected into the vertical from the air temperature change, also masking out the stratosphere:

dt_lapserate = tropo_mask(dta - dts_3d)
dt_lapserate
Loading...

Multiply by the LW temperature kernel and integrate over pressure:

dLW_lapserate = (regr_kernels.lw_t * tropo_mask(dt_lapserate) * dp/100).sum(dim='plev', skipna=True)

Divide by change in GMST to get the feedback:

lapserate_feedback = dLW_lapserate/dgmst
lapserate_feedback.mean(dim='month').plot(cbar_kwargs={'label': 'W m$^{-2}$ K$^{-1}$'})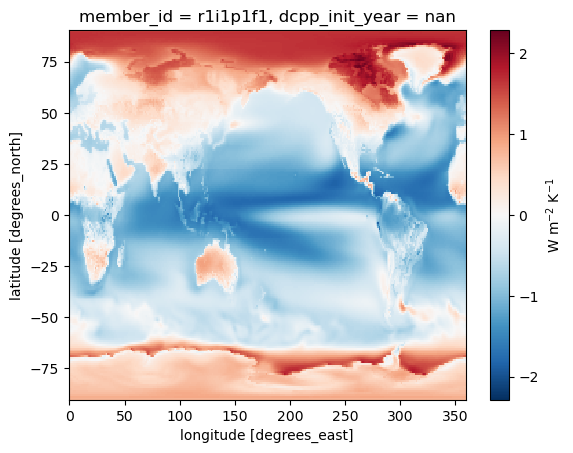
<Figure size 640x480 with 2 Axes>

Global average:

gm_lapserate_feedback = global_average(lapserate_feedback.mean(dim='month')).load()
gm_lapserate_feedback
Loading...

The sum of the Planck and lapse rate feedbacks should equal the full temperature feedback we calculated first:

λPlanck+λLR≈λT\lambda_{\mathrm{Planck}}+\lambda_{\mathrm{LR}}\approx\lambda_T
(7)
(gm_planck_feedback + gm_lapserate_feedback).values, gm_t_feedback.values
(array(-3.68151108), array(-3.64349942))

Water vapor

When calculating the water vapor feedbacks, it is common to use the log difference Δln⁡q=ln⁡qpert−ln⁡qctrl\Delta\ln q=\ln q_{\mathrm{pert}}-\ln q_{\mathrm{ctrl}} instead of the linear difference Δq=qpert−qctrl\Delta q=q_{\mathrm{pert}}-q_{\mathrm{ctrl}}. We also need to normalize the kernels by the log change in specific humidity per unit warming, ∂ln⁡q/∂T\partial\ln q/\partial T. First, we will define a function to calculate the saturation specific humidity (Buck 1981). Note that we want temperature in deg C and pressure in hPa for these formulas to work.

def qs(t, p=None):
    t = t - 273.15
    # Get pressure in hPa
    p = t.plev/100
    
    # Saturation vapor pressure (liquid and ice)
    esl = (1.0007 + 3.46e-6 * p) * 6.1121 * np.exp((17.502 * t) / (240.97 + t))
    esi = (1.0003 + 4.18e-6 * p) * 6.1115 * np.exp((22.452 * t) / (272.55 + t))

    # Convert from vapor pressure to mixing ratio
    wsl = 0.622*esl/(p - esl)
    wsi = 0.622*esi/(p - esi)

    # Use liquid water when temp is above freezing
    ws = xr.where(t > 0, wsl, wsi)

    # Convert to specific humidity
    qs = ws/(1 + ws)

    return qs

We can use the qq and TT from the control and perturbed climates to approximate the normalization factor:

qs_ctrl = qs(ctrl_state.ta.squeeze())
qs_pert = qs(pert_state.ta.squeeze())
dlnqdT = (np.log(qs_pert) - np.log(qs_ctrl))/(pert_state.ta.squeeze() - ctrl_state.ta.squeeze())
dlnqdT
Loading...

Shortwave water vapor

dlnq = np.log(pert_state.hus) - np.log(ctrl_state.hus)
dSW_q = (regr_kernels.sw_q/dlnqdT * dlnq * dp/100).sum(dim='plev')
dSW_q.mean(dim='month').plot()
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in log
  return self.func(*new_argspec)

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in divide
  return self.func(*new_argspec)
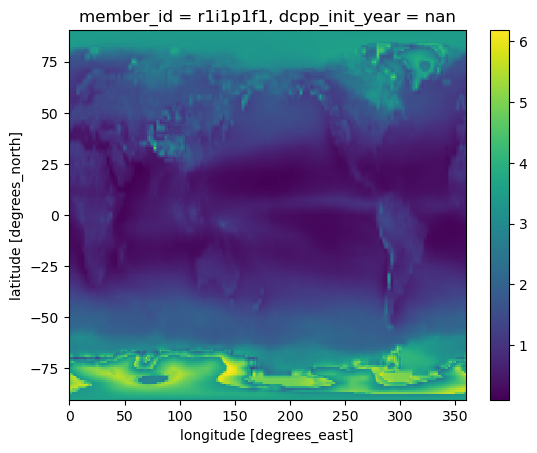
<Figure size 640x480 with 2 Axes>
swq_feedback = dSW_q/dgmst
swq_feedback.mean(dim='month').plot(cbar_kwargs={'label': 'W m$^{-2}$ K$^{-1}$'})
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in log
  return self.func(*new_argspec)

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in divide
  return self.func(*new_argspec)
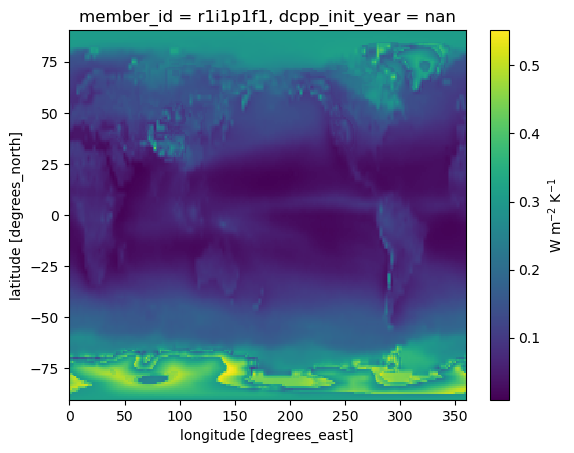
<Figure size 640x480 with 2 Axes>
gm_swq_feedback = global_average(swq_feedback.mean(dim='month')).load()
gm_swq_feedback
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in log
  return self.func(*new_argspec)

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in divide
  return self.func(*new_argspec)
Loading...

Longwave water vapor

dLW_q = (regr_kernels.lw_q/dlnqdT * dlnq * dp/100).sum(dim='plev')
lwq_feedback = dLW_q/dgmst
lwq_feedback.mean(dim='month').plot(cbar_kwargs={'label': 'W m$^{-2}$ K$^{-1}$'})
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in log
  return self.func(*new_argspec)

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in divide
  return self.func(*new_argspec)
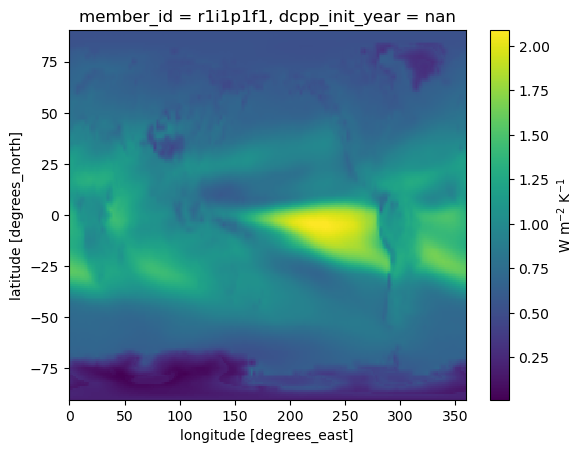
<Figure size 640x480 with 2 Axes>
gm_lwq_feedback = global_average(lwq_feedback.mean(dim='month')).load()
gm_lwq_feedback
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in log
  return self.func(*new_argspec)

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in divide
  return self.func(*new_argspec)
Loading...

Cloud

We will use the Soden et al. (2008) adjustment method to estimate the cloud feedbacks.

Cloud radiative effect

The cloud radiative effect (CRE) is the change in TOA radiation due to the existence of clouds, so it is the difference between all-sky and clear-sky net TOA radiation. We will use the convention that a positive CRE indicates a warming effect of clouds, and a negative CRE indicates a cooling effect of clouds. We therefore need to take note of the sign convention being used for the radiation. Here are the SW TOA radiation variables:

ctrl_state.rsut.mean(dim='month').plot(cbar_kwargs={'label': 'W m$^{-2}$'})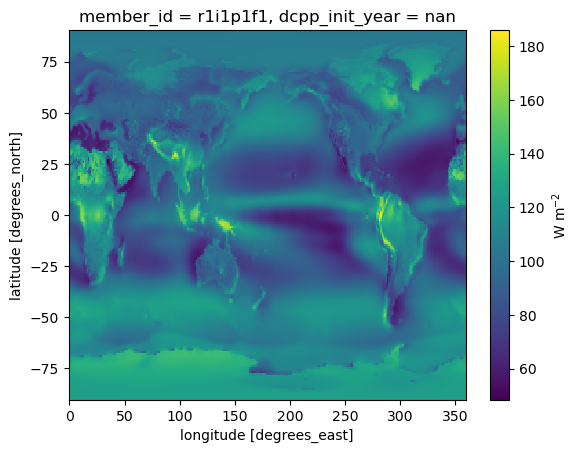
<Figure size 640x480 with 2 Axes>

Positive values for rsut indicate a positive-up convention. For SW we want to compute:

SWCRE=Netall−Netclear=(Downall−Upall)−(Downclear−Upclear)=−Upall+Upclear=−rsut+rsutcs\mathrm{SWCRE}=\mathrm{Net}_{\mathrm{all}}-\mathrm{Net}_{\mathrm{clear}}=(\mathrm{Down}_{\mathrm{all}}-\mathrm{Up}_{\mathrm{all}})-(\mathrm{Down}_{\mathrm{clear}}-\mathrm{Up}_{\mathrm{clear}})=-\mathrm{Up}_{\mathrm{all}}+\mathrm{Up}_{\mathrm{clear}}=-\texttt{rsut}+\texttt{rsutcs}
(8)

where the “Down” terms cancel because clouds have no effect on insolation.

ctrl_SWCRE = -ctrl_state.rsut + ctrl_state.rsutcs
pert_SWCRE = -pert_state.rsut + pert_state.rsutcs
dSWCRE = pert_SWCRE - ctrl_SWCRE

Check the CRE to make sure the sign is correct:

ctrl_SWCRE.mean(dim='month').plot(cbar_kwargs={'label': 'W m$^{-2}$'})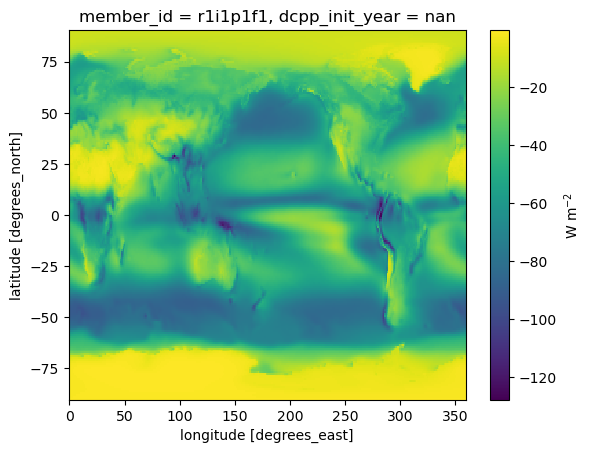
<Figure size 640x480 with 2 Axes>

As expected, negative values indicate that on the SW side, clouds have a cooling effect. Here is the change in SW CRE:

dSWCRE.mean(dim='month').plot(cbar_kwargs={'label': 'W m$^{-2}$'})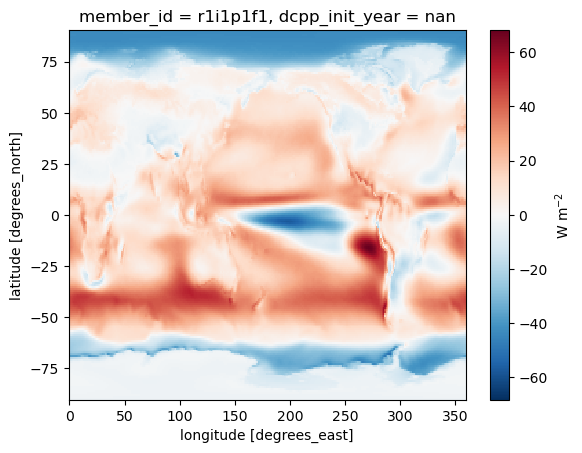
<Figure size 640x480 with 2 Axes>

There is reduced (low) cloud cover under the CO2 forcing, so we can interpret this as clouds cooling the planet less under CO2 forcing, implying a positive feedback. Next, the LW version, where we use TOA outgoing longwave radiation:

ctrl_state.rlut.mean(dim='month').plot(cbar_kwargs={'label': 'W m$^{-2}$'})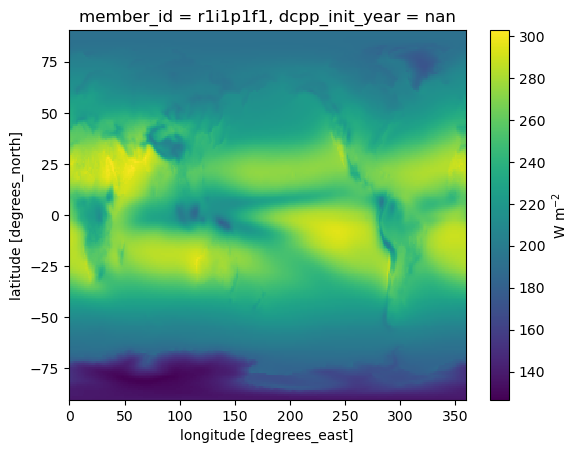
<Figure size 640x480 with 2 Axes>

Positive-up is also used for rlut, so the calculation is similar:

LWCRE=Netall−Netclear=(Downall−Upall)−(Downclear−Upclear)=−Upall+Upclear=−rlut+rlutcs\mathrm{LWCRE}=\mathrm{Net}_{\mathrm{all}}-\mathrm{Net}_{\mathrm{clear}}=(\mathrm{Down}_{\mathrm{all}}-\mathrm{Up}_{\mathrm{all}})-(\mathrm{Down}_{\mathrm{clear}}-\mathrm{Up}_{\mathrm{clear}})=-\mathrm{Up}_{\mathrm{all}}+\mathrm{Up}_{\mathrm{clear}}=-\texttt{rlut}+\texttt{rlutcs}
(9)

where the “Down” terms here are just zero.

ctrl_LWCRE = -(ctrl_state.rlut - ctrl_state.rlutcs)
pert_LWCRE = -(pert_state.rlut - pert_state.rlutcs)
dLWCRE = pert_LWCRE - ctrl_LWCRE
ctrl_LWCRE.mean(dim='month').plot(cbar_kwargs={'label': 'W m$^{-2}$'})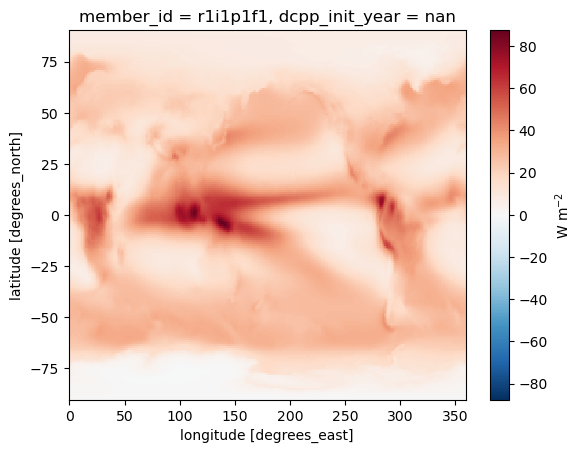
<Figure size 640x480 with 2 Axes>

On the LW side, clouds have a warming effect. Here is the change in LW CRE under the CO2 forcing:

dLWCRE.mean(dim='month').plot(cbar_kwargs={'label': 'W m$^{-2}$'})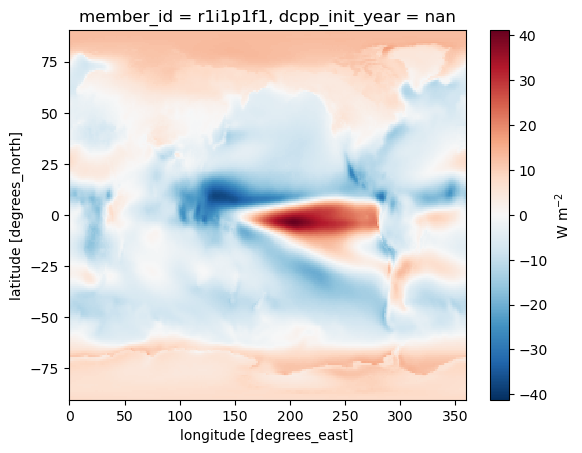
<Figure size 640x480 with 2 Axes>

Adjusting CRE to get cloud feebacks

CRE partially masks some non-cloud feedbacks, so CRE needs to be adjusted to account for this.

Plots

def add_cyclic_point(xarray_obj, dim='lon', period=360):
    if period is None:
        period = xarray_obj.sizes[dim] / xarray_obj.coords[dim][:2].diff(dim).item()
    first_point = xarray_obj.isel({dim: slice(1)})
    first_point.coords[dim] = first_point.coords[dim]+period
    return xr.concat([xarray_obj, first_point], dim=dim)
ann_planck_feedback = planck_feedback.mean(dim='month').load()
ann_lapserate_feedback = lapserate_feedback.mean(dim='month').load()
ann_lwq_feedback = lwq_feedback.mean(dim='month').load()
ann_swq_feedback = swq_feedback.mean(dim='month').load()
/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in log
  return self.func(*new_argspec)

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in divide
  return self.func(*new_argspec)

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in log
  return self.func(*new_argspec)

/home/runner/micromamba/envs/feedback-cookbook-dev/lib/python3.14/site-packages/dask/_task_spec.py:759: RuntimeWarning: invalid value encountered in divide
  return self.func(*new_argspec)

pc0 = ccrs.PlateCarree(central_longitude=0)
pc180 = ccrs.PlateCarree(central_longitude=180)
fig, axs = plt.subplots(2, 2, figsize=(11, 5), dpi=200, subplot_kw=dict(projection=pc180), layout='constrained')

ann_planck_feedback.plot.contourf(ax=axs[0, 0], levels=21, cbar_kwargs=dict(label='W m$^{-2}$ K$^{-1}$'), transform=pc0, cmap='Blues_r')
ann_lapserate_feedback.plot(ax=axs[0, 1], levels=21, cbar_kwargs=dict(label='W m$^{-2}$ K$^{-1}$'), transform=pc0)
ann_swq_feedback.plot(ax=axs[1, 0], levels=21, cbar_kwargs=dict(label='W m$^{-2}$ K$^{-1}$'), transform=pc0, cmap='Reds')
ann_lwq_feedback.plot(ax=axs[1, 1], levels=21, cbar_kwargs=dict(label='W m$^{-2}$ K$^{-1}$'), transform=pc0, cmap='Reds')

for ax in axs.flatten():
    ax.coastlines()

axs[0, 0].set_title('Planck')
axs[0, 1].set_title('Lapse rate')
axs[1, 0].set_title('SW water vapor')
axs[1, 1].set_title('LW water vapor')
fig.suptitle('CESM2 radiative feedbacks (4xCO2 $-$ piControl; ERA5 kernels)', y=1.05)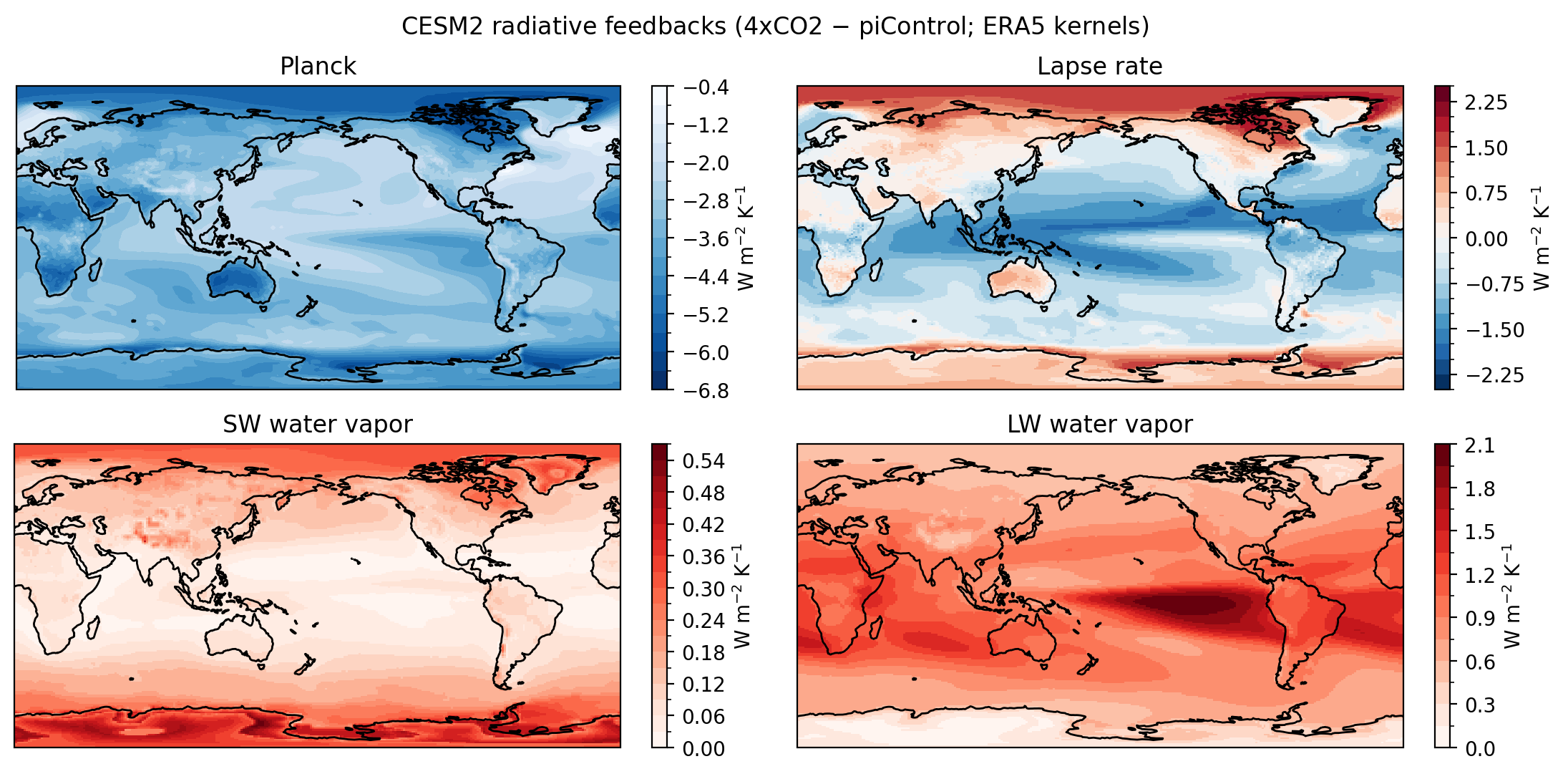
<Figure size 2200x1000 with 8 Axes>
ann_dSWCRE = dSWCRE.mean(dim='month').load()
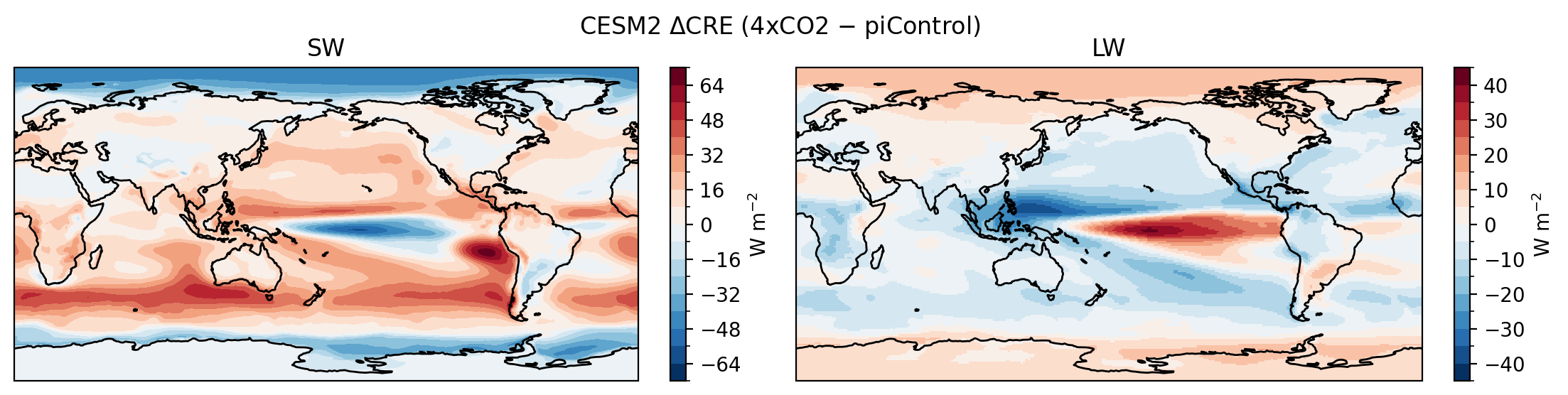
ann_dLWCRE = dLWCRE.mean(dim='month').load()
fig2, axs2 = plt.subplots(1, 2, figsize=(11, 2.5), dpi=200, subplot_kw=dict(projection=pc180), layout='constrained')

ann_dSWCRE.plot.contourf(ax=axs2[0], levels=21, cbar_kwargs=dict(label='W m$^{-2}$'), transform=pc0)
ann_dLWCRE.plot(ax=axs2[1], levels=21, cbar_kwargs=dict(label='W m$^{-2}$'), transform=pc0)

for ax in axs2.flatten():
    ax.coastlines()

axs2[0].set_title('SW')
axs2[1].set_title('LW')
fig2.suptitle('CESM2 $\\Delta$CRE (4xCO2 $-$ piControl)', y=1.05)
<Figure size 2200x500 with 4 Axes>

Summary

What’s next?

Resources

Foundations
Energy Balance Model and Feedbacks
Foundations
Feedbacks with ClimKern