PyWavelets and Jingle Bells

Part 1 for working with audio signals

---

Overview

This notebook will generate a wavelet scalogram to determine the order of notes in a short .wav file. You’ll learn how to generate a Wavelet Power spectrum graph

1. Prerequisites

2. Background

3. PyWavelets Overview

4. Wavelet Power Spectrum

Prerequisites

Concepts	Importance	Notes
Intro to Matplotlib	Necessary	Used to plot data
Intro to Pandas	Necessary	Used to read in and organize data (in particular dataframes)
Intro to Numpy	Necessary	Used to work with large arrays
Intro to SciPy	Helpful	Used to work with .wav files and built-in Fast Fourier Transform

• Time to learn: 20 minutes

---

Background

Wavelet analysis is accomplished in Python via external package. PyWavelets is an open source Python package for wavelet analysis

Either with pip install:

pip install PyWavelets

Or with conda

conda install pywavelets

Imports

import numpy as np                          # working with arrays
import pandas as pd                         # working with dataframes
from scipy.io import wavfile                # loading in wav files
import matplotlib.pyplot as plt             # plot data
from scipy.fftpack import fft, fftfreq      # working with Fourier Transforms

import pywt                                 # PyWavelets

PyWavelets Overview

PyWavelets returns both the coefficients and frequency information for wavelets from the input data

coeffs, frequencies = pywt.cwt(data, scales, wavelet, sampling_period)

Input Values

The Continuous Wavelet Transform (CWT) in PyWavelets accepts multiple input values:

Required:

• data: input data (as an array)

• wavelet: name of the Mother wavelet

• scales: collection of the scales to use will determine the range which the wavelet will be stretched or squished

Optional:

• sampling_period: sampling period for frequencies output. Scales are not scaled by the period (and coefficients are independent of the sampling_period)

Return Values

The continuous wavelet transforms in PyWavelets returns two values:

• coefficients: collection of complex number outputs for wavelet coefficients

• frequencies: collection of frequencies (if the sampling period are in seconds then frequencies are in hertz otherwise a sampling period of 1 is assumed)

The final size of coefficients depends on the length of the input data and the length of the given scales.

Choosing a Scale

Scales vs. Frequency

The range of scales are a combination of the smallest scale (s0), spacing between discrete scales (dj), and the maximum scale (jtot).

For the purpose of this exercise, the musical range of frequencies range from 261 - 494 Hz.

Note	Freq
A note	440 hz
B note	494 hz
C note	261 hz
D note	293 hz
E note	330 hz
F note	350 hz
G note	392 hz

Note: Musical note frequencies can vary, these frequencies are taken from here

It is good practice to include a range greater than precisely needed. This will make the bands for each frequency in the wavelets clearer.

Scales will change the shape of the wavelet to have it match a specific frequency. For example, scalings from 1 to 40 represent a frequency range from 8125 - 208.33 Hz.

sample_rate, signal_data = wavfile.read('jingle_bells.wav')
scales = np.arange(1, 40)
wavelet_coeffs, freqs = pywt.cwt(signal_data, scales, wavelet = "morl")

Extract audio .wav file

The .wav input file contains information about the amplitude at every time step (in seconds) in the file. The frequency will determine which note each part of the piece represents.

sampleRate, signalData = wavfile.read("../data/jingle_bells.wav")

duration = len(signalData) / sampleRate
time = np.arange(0, duration, 1/sampleRate) 

print(f"Sample Rate: {sampleRate}")
print(f"duration = {duration} seconds")
print(f"Total Length in time steps = {len(time)}")

Sample Rate: 10000
duration = 15.6991 seconds
Total Length in time steps = 156991

Let’s Give the Data a Look!

It is always good practice to view the data that we have collected. First, let’s organize the data into a pandas dataframe to organize the amplitude and time stamps.

signal_df = pd.DataFrame({'time (seconds)': time, 'amplitude': signalData})
signal_df.head()

	time (seconds)	amplitude
0	0.0000	-417
1	0.0001	-2660
2	0.0002	-2491
3	0.0003	6441
4	0.0004	-8540

Plot a Small Sample of the .wav File

Plot a small subsample of the .wav to visualize the input data.

fig, ax = plt.subplots(figsize=(8, 8))
fig = plt.plot(signal_df["time (seconds)"], signal_df["amplitude"])
plt.title("Subsample of \"Jingle Bells\" Audio File")
ax.set_xlim(signal_df["time (seconds)"][2000], signal_df["time (seconds)"][3000])
plt.xlabel("Time (seconds)")
plt.ylabel("Amplitude")
plt.show()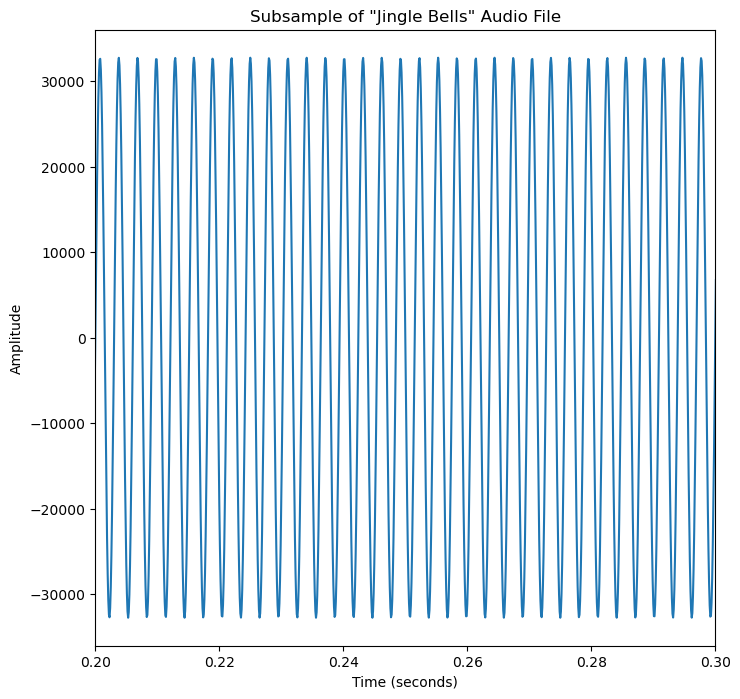

Power Spectrum

wavelet_coeffs is a complex number with a real and an imaginary part (1 + 2i). The power spectrum plots the real component of the complex number. The real component represents the magnitude of the wavelet coefficient displayed as the absolute value of the coefficients squared.

wavelet_mother = "morl" # morlet mother wavelet

# scale determines how squished or stretched a wavelet is
scales = np.arange(1, 40)
wavelet_coeffs, freqs = pywt.cwt(signalData, scales, wavelet = wavelet_mother)

# Shape of wavelet transform
print(f"size {wavelet_coeffs.shape} with {wavelet_coeffs.shape[0]} scales and {wavelet_coeffs.shape[1]} time steps")
print(f"x-axis be default is: {wavelet_coeffs.shape[1]}")
print(f"y-axis be default is: {wavelet_coeffs.shape[0]}")

size (39, 156991) with 39 scales and 156991 time steps
x-axis be default is: 156991
y-axis be default is: 39

A Note on Choosing the Right Scales

freqs is normalized frequencies, so it needs to be multiplied by this sampling frequency to turn it back into frequencies which means that you need to multiply them by your sampling frequency (500Hz) to turn them into actual frequencies.

wavelet_mother = "morl" # morlet mother wavelet

# scale determines how squished or stretched a wavelet is
scales = np.arange(1, 40)
wavelet_coeffs, freqs = pywt.cwt(signalData, scales, wavelet = wavelet_mother)

plt.axhline(y=440, color='lightpink', linestyle='--', label='A') # A note: 440 hz
plt.axhline(y=494, color="lightblue", linestyle='--', label='B') # B Note: 494 hz
plt.axhline(y=261, color='red', linestyle='--', label='C')       # C Note: 261 hz
plt.axhline(y=293, color='green', linestyle='--', label='D')     # D Note: 293 hz
plt.axhline(y=330, color='orange', linestyle='--', label='E')    # E Note: 330 hz
plt.axhline(y=350, color='grey', linestyle='--', label='F')      # F Note: 350 hz
plt.axhline(y=392, color='purple', linestyle='--', label='G')    # G Note: 392 hz

plt.xlabel("Scale")
plt.ylabel("Frequency (Hz)")
print(f"Frequency in Hz:\n{freqs*sampleRate}")
plt.plot(freqs*sampleRate)

Frequency in Hz:
[8125.         4062.5        2708.33333333 2031.25       1625.
 1354.16666667 1160.71428571 1015.625       902.77777778  812.5
  738.63636364  677.08333333  625.          580.35714286  541.66666667
  507.8125      477.94117647  451.38888889  427.63157895  406.25
  386.9047619   369.31818182  353.26086957  338.54166667  325.
  312.5         300.92592593  290.17857143  280.17241379  270.83333333
  262.09677419  253.90625     246.21212121  238.97058824  232.14285714
  225.69444444  219.59459459  213.81578947  208.33333333]

[<matplotlib.lines.Line2D at 0x7f2225867b50>]

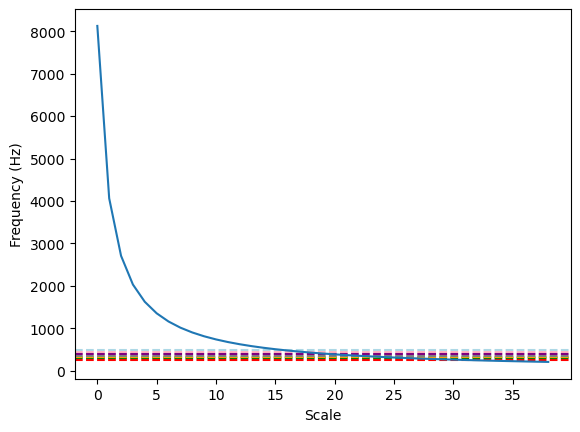
Plot scalogram

The scalogram will visually display the strength of the frequency at a particular time interval. A stronger signal in red represents a wavelet that strongly matches a specific frequency in that range, while blue represents where the wavelet has a weaker match to a specific frequency. The best match for a note will be found where the signal is strongest.

fig, ax = plt.subplots(figsize=(8, 8))
data = np.log2(np.square(abs(wavelet_coeffs))) # compare the magnitude
plt.xlabel("Time Steps")
plt.ylabel("Scale Sensitivity")
plt.imshow(data, 
           vmax=(data).max(), vmin=(data).min(),
           cmap="coolwarm", aspect="auto")
plt.colorbar()
plt.show()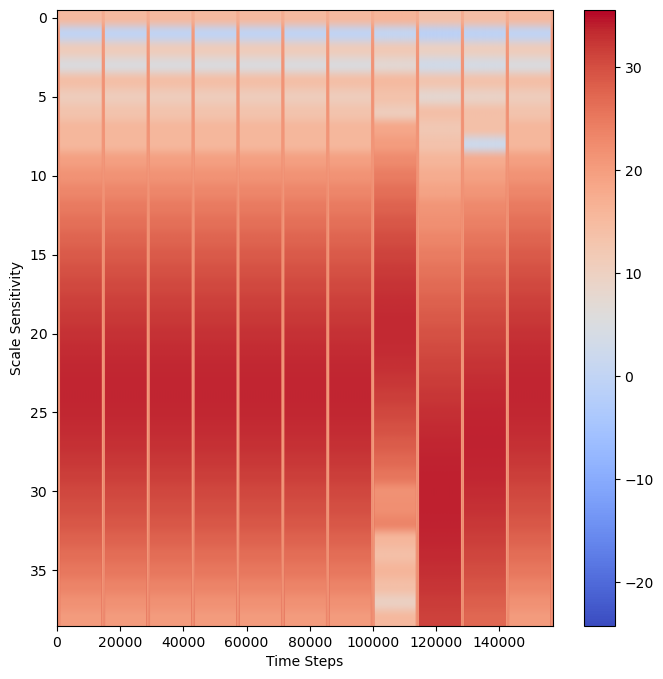

Overlay Possible Frequencies

To overlay these frequencies with the wavelet scalogram:

Important Note

To convert HZ frequency to a scale = hz *.0001 (where 0.01 is 100 Hz sampling) then apply frequency2scale() PyWavelets function

fig, ax = plt.subplots(figsize=(8, 8))

# Overlay frequency of notes as dotted lines
sample_rate = 1/sampleRate
a_freq = pywt.frequency2scale(wavelet_mother, 440*sample_rate)
plt.axhline(y=a_freq, color='lightpink', linestyle='--', label='A') # A note: 440 hz
b_freq = pywt.frequency2scale(wavelet_mother, 494*sample_rate)
plt.axhline(y=b_freq, color="lightblue", linestyle='--', label='B') # B Note: 494 hz
c_freq = pywt.frequency2scale(wavelet_mother, 261*sample_rate)
plt.axhline(y=c_freq, color='red', linestyle='--', label='C')       # C Note: 261 hz
d_freq = pywt.frequency2scale(wavelet_mother, 293*sample_rate)
plt.axhline(y=d_freq, color='green', linestyle='--', label='D')     # D Note: 293 hz
e_freq = pywt.frequency2scale(wavelet_mother, 330*sample_rate)
plt.axhline(y=e_freq, color='orange', linestyle='--', label='E')    # E Note: 330 hz
f_freq = pywt.frequency2scale(wavelet_mother, 350*sample_rate)
plt.axhline(y=f_freq, color='grey', linestyle='--', label='F')      # F Note: 350 hz
g_freq = pywt.frequency2scale(wavelet_mother, 392*sample_rate)
plt.axhline(y=g_freq, color='purple', linestyle='--', label='G')    # G Note: 392 hz

# Plot Power scalogram
power = np.log2(np.square(abs(wavelet_coeffs))) # compare the magntiude
plt.title("Note Frequency as Scale")
plt.xlabel("Time Steps")
plt.ylabel("Scale Sensitivity")
plt.imshow(power, 
           vmax=(power).max(), vmin=(power).min(),
           cmap="coolwarm", aspect="auto")
plt.legend()
plt.show()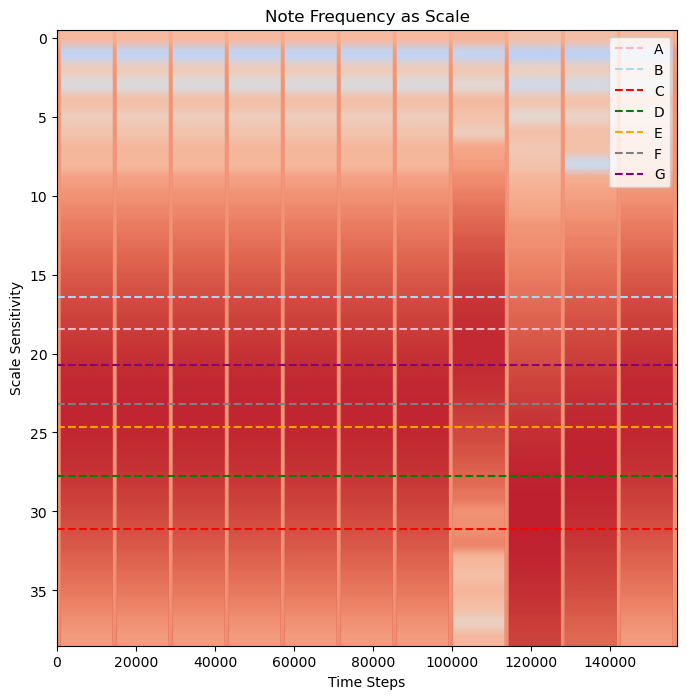

Determining Which Frequencies to Overlay

For this example, we know that the input data is “Jingle Bells” so we know which notes are going to be used.

"Jingle Bells, Jingle Bells, Jingle All the Way" as EEE EEE EGCDE

However, let’s imagine that we aren’t sure. Wavelets gain information about when a frequency occurs, but at a lower resolution to an exact frequency. To determine which notes are a best fit, you can make use of FFT to determinine which notes to include. Without FFT, the larger possible ranges of frequency can make it possible to confuse nearby notes.

Fast Fourier Transform

fourier_transform = abs(fft(signalData))
freqs = fftfreq(len(fourier_transform), sample_rate)

fig, ax = plt.subplots(figsize=(8, 8))
plt.plot(freqs, fourier_transform)
ax.set_xlim(left=200, right=500) 
plt.axvline(x=261, color="red", label="C",alpha=0.5)    # C Note: 261 hz
plt.axvline(x=293, color="green", label="D",alpha=0.5)  # D Note: 293 hz
plt.axvline(x=330, color="orange", label="E",alpha=0.5) # E Note: 330 hz
plt.axvline(x=391, color="purple", label="G",alpha=0.5) # G Note: 391 hz
plt.title("Signal Frequency Prevalence (FFT)")
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.legend()
plt.show()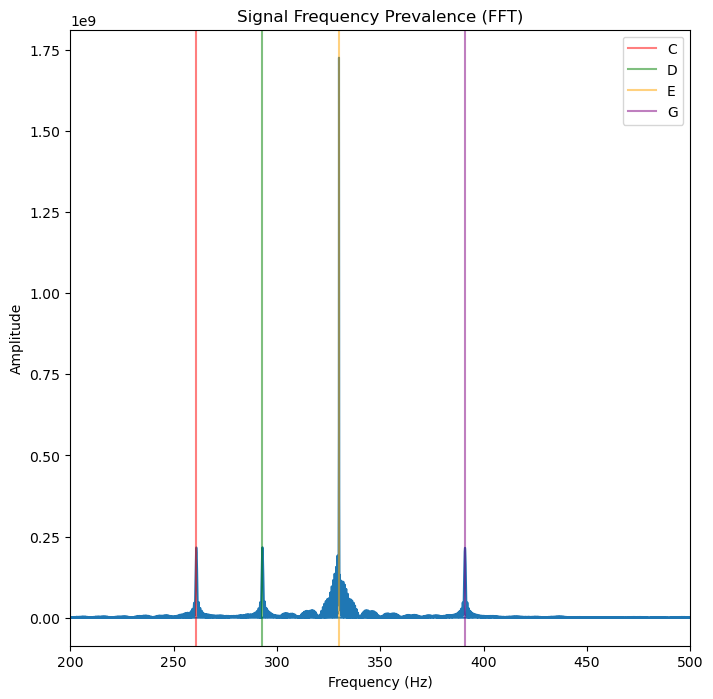

Overlay Frequency of Notes

Using FFT we can now say that there are four clear frequencies that are associated with four notes for CDEG.

Fast Fourier Transform Predicts Four Notes

FFT predicts an output with four notes:

C, D, E, G

Let’s plot the notes!

fig, ax = plt.subplots(figsize=(8, 8))

# Overlay frequency of notes as dotted lines
sample_rate = 1/sampleRate
c_freq = pywt.frequency2scale(wavelet_mother, 261*sample_rate)
plt.axhline(y=c_freq, color='red', linestyle='--', label='C')       # C Note: 261 hz
d_freq = pywt.frequency2scale(wavelet_mother, 293*sample_rate)
plt.axhline(y=d_freq, color='green', linestyle='--', label='D')     # D Note: 293 hz
e_freq = pywt.frequency2scale(wavelet_mother, 330*sample_rate)
plt.axhline(y=e_freq, color='orange', linestyle='--', label='E')    # E Note: 330 hz
g_freq = pywt.frequency2scale(wavelet_mother, 392*sample_rate)
plt.axhline(y=g_freq, color='purple', linestyle='--', label='G')    # G Note: 392 hz

# Plot Power scalogram
power = np.log2(np.square(abs(wavelet_coeffs))) # compare the magntiude
plt.title("Note Frequency as Scale")
plt.xlabel("Time Steps")
plt.ylabel("Scale Sensitivity")
plt.imshow(power, 
           vmax=(power).max(), vmin=(power).min(),
           cmap="coolwarm", aspect="auto")
plt.legend()
plt.show()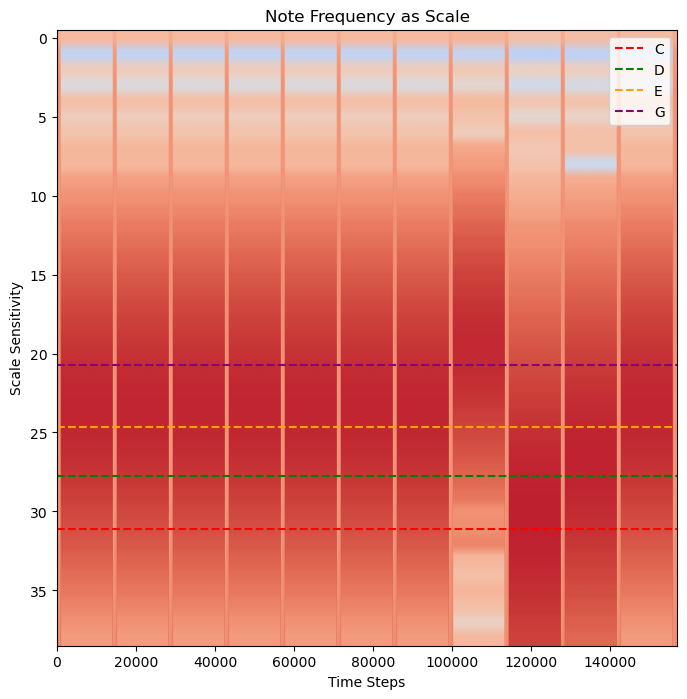

Four Notes!

The darkest color correlates with the frequency at each time stamp. Rather than appearing as distinct peaks like a Fourier Transform, wavelets return a gradient of frequencies. This is the loss in precision due to Heisenberg’s Uncertainty Principle. While the frequencies can still be determined, there is some level of uncertainty in the exact frequencies. This is where combining wavelets with a Fourier Transform can be useful. We now know that this piece has four notes CDEG. The vertical bands represent where the note ends before the next note begins. This piece of music has a deliberate start and stop so this band will not always be as obvious in other pieces of music.

We can read this wavelet analysis by finding what note corresponds with the darkest band.

We should now have the order of the notes, read from left to right:

EEE EEE EGCDE

---

Summary

Wavelets can report on both the frequency and time a frequency occurs. However, due to Heisenberg’s Uncertainty Principle, by gaining resolution on time, some resolution on frequency is lost. It can be helpful to incorporate both a Fourier Transform and a Wavelet analysis to a signal to help determine the possible ranges of expected frequencies. PyWavelets is a free open-source package for wavelets in Python.

What’s next?

Up next: apply wavelets transform to determine the frequency and order of an unknown input!