Skip to article frontmatterSkip to article content

Great Circles and a Point

Authors
Affiliations
NSF National Center for Atmospheric Research

A hockey puck is launched from London toward the west, on a stationary earth. The natural great circle motion of the puck takes it toward the equator, not along the original line of latitude, which we might normally call west. The great circle path also coincides with the line of sight toward the west (projected radially down to the earth'surface). Thus we must conclude that Costa Rica is due west of London. Credit: Oregon State (https://sites.science.oregonstate.edu/~mcintyre/coriolis/Curvilinear_GIF.html)

Great Circles and a Point

Overview

Oh no! A plane traveling across the country suddenly discovers it is low on fuel! It can no longer make it to the planned airport, instead it has to find the closest airport to its current position that it can make it with its remaining fuel.

In great circle terms, we want to determine how far a point (let’s say, the next closest airport) is from a great circle arc (the flight’s path). In this notebook we will:

  1. Determine the distance of a point to a great circle arc (cross-track and along-track distance)

  2. Determine if a point lies on a great circle arc and path (with and without tolerances)

Prerequisites

ConceptsImportanceNotes
NumpyNecessaryUsed to work with large arrays
PandasNecessaryUsed to read in and organize data (in particular dataframes)
Intro to CartopyHelpfulWill be used for adding maps to plotting
MatplotlibHelpfulWill be used for plotting

  • Time to learn: 20 minutes

Imports

  • Import Packages

  • Setup location dataframe with coordinates

import pandas as pd                                    # read in data text file
import numpy as np                                     # working with degrees and radians

from pyproj import Geod                                # working with the Earth as an ellipsod (WGS-84)
import geopy.distance                                  # moving along a known distance on the Earth's ellipsoid surface

import matplotlib.pyplot as plt                        # plotting a graph
from cartopy import crs as ccrs, feature as cfeature   # plotting a world map
# Get all Coordinates for Locations
location_df = pd.read_csv("../location_full_coords.txt")
location_df = location_df.rename(columns=lambda x: x.strip()) # strip excess white space from column names and values
location_df.index = location_df["name"]
location_df.head()
Loading...

Determine the distance of a point to a great circle arc

The distance from a point to a great circle arc is known as the cross track distance (sometimes known as cross track error). For example, how far would a plane have to fly from its path to get to an unscheduled airport for refueling? Meantime, the along track distance measures how far along the great arc a point lies. For instance, what is your new position (latitude/longitude) when you’ve traveled 250 km into your 2000 km plane ride?

  • Cross track distance: angular distance from point P to great circle path

  • Along track distance: angular distance along the great circle path from A to B before hitting a point that is closest to point P

geodesic = Geod(ellps="WGS84")
earth_radius = 6378137  # meters

Cross Track Distance

Distance of a point to a great circle arc is defined as:

dxt=asin(sin(δ13)⋅sin(θ13−θ12))∗Rdxt = asin( sin(δ13) ⋅ sin(θ13 − θ12) ) * R
(1)

Where,

  • δ13 (delta_13) is (angular) distance from start point to third point

  • θ13 (theta_13) is (initial) bearing from start point to third point

  • θ12 (theta_12) is (initial) bearing from start point to end point

  • R is the earth’s radius

Then,

dxt=np.arcsin(np.sin(delta13)∗np.sin(theta13−theta12))∗Rd_xt = np.arcsin(np.sin(delta_13)*np.sin(theta_13 - theta_12)) * R
(2)
XTD=asin(sin(distAD)∗sin(crsAD−crsAB))XTD =asin(sin(dist_AD)*sin(crs_AD-crs_AB))
(3)

Where,

  • Positive Cross-Track Distance: Point lies in the hemisphere to the left of the great circle

  • Negative Cross-Track Distance: Point lies in the hemiphere to the right of the great circle

Note: If the point A is the North or South Pole replace crs_AD-crs_AB with lon_D-lon_B or lon_B-lon_D, respectively

That was a lot of math, let’s see how that translates into a Python function. For the purpose of this example, let’s determine the forward bearing and distance between the great circle arc and the new point on an ellipsoid.

We will be creating two sides of a spherical triangle. Side 1 will be the great circle arc formed from Point A to Point B, while Side 2 will be a new great circle arc we will create from Point A to the new point C. We can use the angle—angular distance—between these two legs to determine the cross track distance:

def cross_track_distance(start_point=None, end_point=None, new_point=None):
    # Determine the forward bearing from Point A (start) to Point B (end)
    fwd_bearing_start_end, _, _ = geodesic.inv(location_df.loc[start_point, "longitude"],
                                               location_df.loc[start_point, "latitude"],
                                               location_df.loc[end_point, "longitude"],
                                               location_df.loc[end_point, "latitude"])
    
    # Determine the forward bearing (angle) and distance from Point A (start) to new Point C
    fwd_bearing_start_new, _, distance_m_start_new = geodesic.inv(location_df.loc[start_point, "longitude"],
                                                                  location_df.loc[start_point, "latitude"],
                                                                  location_df.loc[new_point, "longitude"],
                                                                  location_df.loc[new_point, "latitude"]) 

    # Determine the Angular Distance from Point A to Point C
    angular_distance_start_new = distance_m_start_new / earth_radius
    ct_distance = np.arcsin(np.sin(angular_distance_start_new) * np.sin(np.deg2rad(fwd_bearing_start_new - fwd_bearing_start_end))) * earth_radius
    return ct_distance

Along Track Distance

Imagine a great circle arc that will appear like: A -------- C -------------------B, where the distance along the great circle arc (created from Point A to B) from Point A to Point C is the along-track distance.

This is defined as:

dat=acos(cos(δ13)cos(δxt))∗Rdat = acos(\frac{cos(δ13)}{cos(δxt)}) * R
(4)

  • δ13 (delta_13) is (angular) distance from start point to third point

  • δxt (delta_xt) is (angular) cross-track distance

  • R is the earth’s radius

So,

dat=np.arccos(np.cos(delta13)np.cos(dxt/R)∗Rd_at = np.arccos(\frac{np.cos(delta_13)}{np.cos(d_xt/R)} * R
(5)
ATD=acos(cos(distAD)cos(XTD))ATD=acos(\frac{cos(dist_AD)}{cos(XTD)})
(6)

However, for very short distances we can also use a new equation that is less susceptible to rounding errors:

ATD=asin(sin(distAD))2−(sin(XTD))2)cos(XTD)ATD=asin(\sqrt{\frac{sin(dist_AD))^2 - (sin(XTD))^2 )}{cos(XTD)}}
(7)

To similarly convert into a Python function, we will need to know the total length of the great circle arc from Point A to Point B. We will also measure the distance from the Point A to the new Point C along the great circle arc from Point A to Point B.

def along_track_distance(start_point=None, end_point=None, new_point=None):
    # Determine the cross track distance from Point A to Point B from Point C
    crosst_distance = cross_track_distance(start_point, end_point, new_point)

    # Determine the total distance of a great circle arc from Point A to Point C
    _, _, distance_m_start_new = geodesic.inv(location_df.loc[start_point, "longitude"],
                                              location_df.loc[start_point, "latitude"],
                                              location_df.loc[new_point, "longitude"],
                                              location_df.loc[new_point, "latitude"])  
    
    # Determine the Along-Track Distance using the Cross Track Distance Distance 
    angular_distance_start_new = distance_m_start_new / earth_radius
    at_distance = np.arccos(np.cos(angular_distance_start_new) / np.cos(crosst_distance / earth_radius)) * earth_radius
    return at_distance

Determine Closest Point along Great Circle Arc

To be able to plot a cross track distance we need to find the point on the great circle that is closest to the new Point C. To do this we need to find the closest point from Point C to the arc and measure the along track distance that the intersection lies

# Distance point along great circle path
def point_along_path(start_point=None, end_point=None, distance_m=None):
    fwd_bearing, _, _ = geodesic.inv(location_df.loc[start_point, "longitude"],
                                     location_df.loc[start_point, "latitude"],
                                     location_df.loc[end_point, "longitude"],
                                     location_df.loc[end_point, "latitude"])  
    origin = geopy.Point(location_df.loc[start_point, "latitude"],
                         location_df.loc[start_point, "longitude"])
    distance_to_move = geopy.distance.distance(
                            kilometers=distance_m / 1000)  # distance to move towards the next point
    final_position = distance_to_move.destination(origin, bearing=fwd_bearing)
    return (final_position.latitude, final_position.longitude)

Let’s see how of this looks on a map! Let’s plot!

In the previous notebook, we determined how to interpolate points along the great circle arc (interpolate_points_along_gc and arc_points). We will repeat the functions below to be able to use them to plot the great circle arc with the new information about cross-track and along-track distances

# See Previous Notebook for how these functions were defined

def interpolate_points_along_gc(lat_start,
                                lon_start,
                                lat_end,
                                lon_end,
                                distance_between_points_meter): 
    lat_lon_points = [(lat_start, lon_start)]
    
    # move to next point when distance between points is less than the equal distance
    move_to_next_point = True
    while(move_to_next_point):
        forward_bearing, reverse_bearing, distance_meters = geodesic.inv(lon_start,
                                                                         lat_start, 
                                                                         lon_end,
                                                                         lat_end)
        if distance_meters < distance_between_points_meter:
            # ends before overshooting
            move_to_next_point = False
        else:
            start_point = geopy.Point(lat_start, lon_start)
            distance_to_move = geopy.distance.distance(
                            kilometers=distance_between_points_meter /
                            1000)  # distance to move towards the next point
            final_position = distance_to_move.destination(
                            start_point, bearing=forward_bearing)
            lat_lon_points.append((final_position.latitude, final_position.longitude))
            # new starting position is newly found end position
            lon_start, lat_start = final_position.longitude, final_position.latitude
    lat_lon_points.append((lat_end, lon_end))
    return lat_lon_points

def arc_points(start_lat=None,
               start_lon=None,
               end_lat=None,
               end_lon=None,
               n_total_points=10):
    _, _, distance_meter =  geodesic.inv(start_lon,
                                        start_lat,
                                        end_lon,
                                        end_lat)
        
    distance_between_points_meter = distance_meter / (n_total_points + 1)

    
    new_points_lst = interpolate_points_along_gc(start_lat,
                                              start_lon,
                                              end_lat,
                                              end_lon,
                                              distance_between_points_meter)
    return new_points_lst

To begin, we will plot the cross track distance. This will look like a map with two arcs: one from Point A to Point B (the primary great circle arc) and a second that will show the angular distance between the great circle arc and a new point

def plot_cross_track(start_point=None, end_point=None, new_point=None,
                     lon_west=-130, lon_east=-60,
                     lat_south=20, lat_north=60):
    # Set up world map plot
    fig = plt.subplots(figsize=(16, 10))
    projection_map = ccrs.PlateCarree()
    ax = plt.axes(projection=projection_map)
    ax.set_extent([lon_west, lon_east, lat_south, lat_north], crs=projection_map)
    ax.coastlines(color="black")
    ax.add_feature(cfeature.BORDERS, edgecolor='grey')
    ax.add_feature(cfeature.STATES, edgecolor="grey")

    # Cross-Track and Along-Track Distances
    ct_distance = cross_track_distance(start_point, end_point, new_point)
    print(f"Cross Track Distance: \n{ct_distance} meters ({ct_distance/1000} km)")

    at_distance = along_track_distance(start_point, end_point, new_point)
    print(f"Along Track Distance: \n{at_distance} meters ({at_distance/1000} km)\n")

    closest_point = point_along_path(start_point, end_point, at_distance)
    print(f"Closest Point To Point Along Great Circle Path:\n{closest_point}") 

    # Plot Latitude/Longitude Points of the Great Circle Arc (with 10 interpolate points)
    great_circle_arc_pts = arc_points(location_df.loc[start_point, "latitude"],
                                      location_df.loc[start_point, "longitude"],
                                      location_df.loc[end_point, "latitude"],
                                      location_df.loc[end_point, "longitude"],
                                      10)
    longitudes = [x[1] for x in great_circle_arc_pts] # longitude
    latitudes = [x[0] for x in great_circle_arc_pts] # latitude
    plt.plot(longitudes, latitudes, c="purple")
    plt.scatter(longitudes, latitudes, c="purple")

    # Plot the Cross Track Distance as an Arc from Point C to the closest point on the arc (Point D) (with 10 intrpolated points)
    cross_track_arc = arc_points(closest_point[0],
                                 closest_point[1],
                                 location_df.loc[new_point, "latitude"],
                                 location_df.loc[new_point, "longitude"],
                                   10)
    longitudes = [x[1] for x in cross_track_arc] # longitude
    latitudes = [x[0] for x in cross_track_arc] # latitude
    plt.plot(longitudes, latitudes, c="green")
    plt.scatter(longitudes, latitudes, c="green")

    # Plot the Closest Point on the Arc in Red (to see easier)
    plt.scatter(closest_point[1], closest_point[0], c="red")

    plt.title(f"Closest Point {closest_point} from {start_point.title()}->{end_point.title()} to {new_point.title()}, Cross-Track Distance = {ct_distance/1000:4f} km")
    plt.show()

  • Positive Cross-Track Distance: Point lies in the hemisphere to the left of the great circle

  • Negative Cross-Track Distance: Point lies in the hemiphere to the right of the great circle

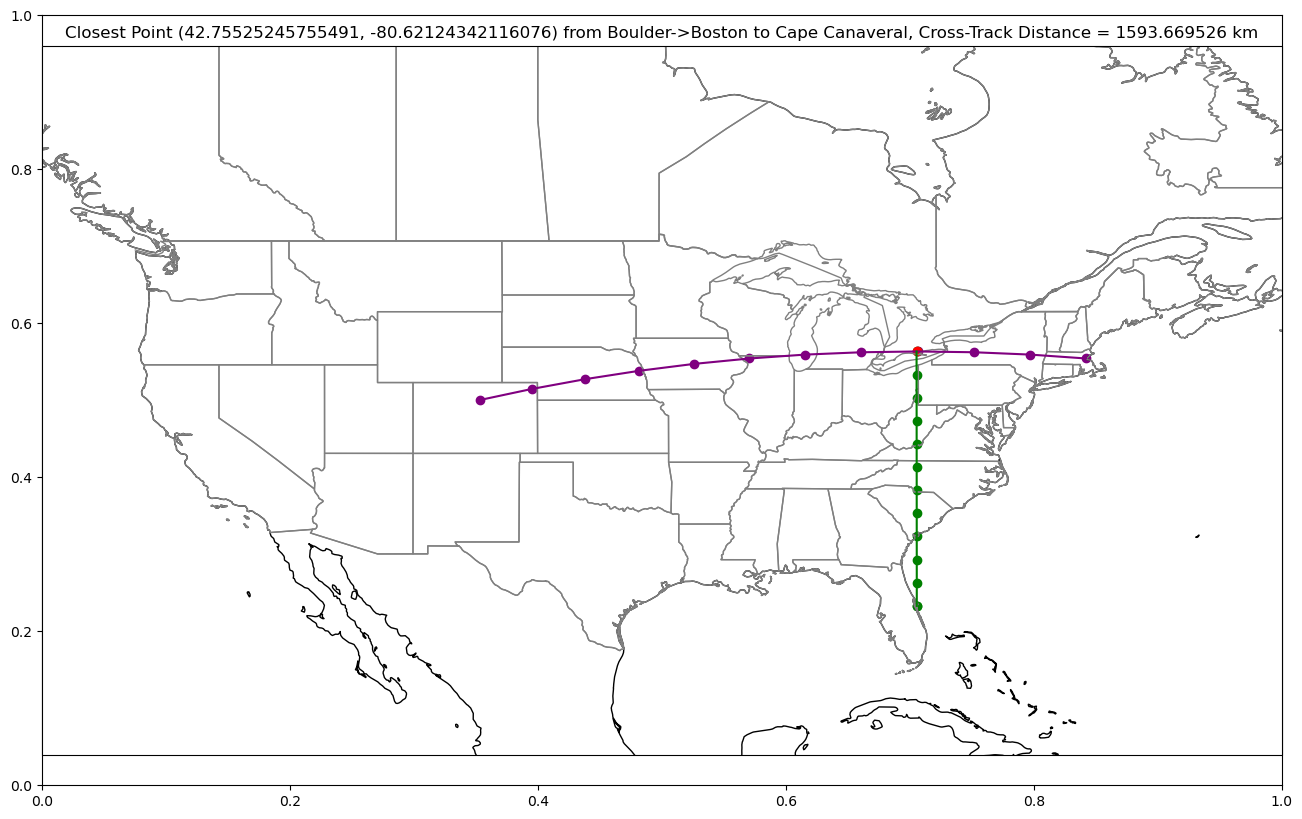
plot_cross_track(start_point="boulder", end_point="boston", new_point="cape canaveral")
Cross Track Distance: 
1593669.526094791 meters (1593.669526094791 km)
Along Track Distance: 
2076501.5510165778 meters (2076.5015510165777 km)

Closest Point To Point Along Great Circle Path:
(42.75525245755491, -80.62124342116076)

/home/runner/micromamba/envs/cookbook-gc/lib/python3.13/site-packages/cartopy/io/__init__.py:242: DownloadWarning: Downloading: https://naturalearth.s3.amazonaws.com/50m_physical/ne_50m_coastline.zip
  warnings.warn(f'Downloading: {url}', DownloadWarning)

/home/runner/micromamba/envs/cookbook-gc/lib/python3.13/site-packages/cartopy/io/__init__.py:242: DownloadWarning: Downloading: https://naturalearth.s3.amazonaws.com/50m_cultural/ne_50m_admin_0_boundary_lines_land.zip
  warnings.warn(f'Downloading: {url}', DownloadWarning)

/home/runner/micromamba/envs/cookbook-gc/lib/python3.13/site-packages/cartopy/io/__init__.py:242: DownloadWarning: Downloading: https://naturalearth.s3.amazonaws.com/50m_cultural/ne_50m_admin_1_states_provinces_lakes.zip
  warnings.warn(f'Downloading: {url}', DownloadWarning)
<Figure size 1600x1000 with 2 Axes>

Determine if a point lies on a great circle arc and path

Does a given Point C lie on a great circle arc? Does it lie on the great circle path? We can check if a point lies on a great circle path/arc if:

  • Check if the latitude/longtiude matches the expected latitude that the same longitude position would have produced on the great circle path

This is possible with and without tolerances (in meters) to allow for some grace based on your precision.

def is_point_on_arc(start_point=None, end_point=None,
                check_point=None, tolerance=0):
    # tolerance in meters
    lon1 = np.deg2rad(location_df.loc[start_point, "longitude"])
    lat1 = np.deg2rad(location_df.loc[start_point, "latitude"])
    lon2 = np.deg2rad(location_df.loc[end_point, "longitude"])
    lat2 = np.deg2rad(location_df.loc[end_point, "latitude"])
    check_lon = np.deg2rad(location_df.loc[check_point, "longitude"])
    check_lat = np.deg2rad(location_df.loc[check_point, "latitude"])

    # Verify not meridian (longitude passes through the poles)
    if np.sin(lon1 - lon2) == 0:
        print("Invalid inputs: start/end points are meridians")
        return np.nan
    
    # verify not antipodal (diametrically opposite, points)
    if lat1 + lat2 == 0 and abs(lon1-lon2) == np.pi:
        print("Invalid inputs: start/end points are antipodal")
        return np.nan

    # account for tolerance based on cross-track distance from arc
    ct_distance = cross_track_distance(start_point, end_point, check_point)
    print(f"Cross-Track Distance = {ct_distance} meters")
    if np.abs(ct_distance) <= tolerance:
        return True

    # determine expected latitude
    num = np.sin(lat1)*np.cos(lat2)*np.sin(check_lon-lon2)-np.sin(lat2)*np.cos(lat1)*np.sin(check_lon-lon1)
    den = np.cos(lat1)*np.cos(lat2)*np.sin(lon1-lon2)
    new_lat = np.arctan(num/den)
    expected_lat = np.rad2deg(new_lat)
    return bool(check_lat == expected_lat)

Check if a point lies on a great circle arc

Let’s see this for ourselves. Does the city of Rockford lie on the great circle arc from Boulder to Boston?

is_point_on_arc("boulder", "boston", "rockford", tolerance=0) # with no tolerance (0 meters)
Cross-Track Distance = 18201.48035911659 meters
False

Rockford is sitting about 18 km away from the great circle arc that is formed by Boulder and Boston. Let’s give it a look on a map:

plot_cross_track(start_point="boulder", end_point="boston", new_point="rockford")
Cross Track Distance: 
18201.48035911659 meters (18.20148035911659 km)
Along Track Distance: 
1378654.5186233742 meters (1378.654518623374 km)

Closest Point To Point Along Great Circle Path:
(42.434120910748035, -89.11630028269337)
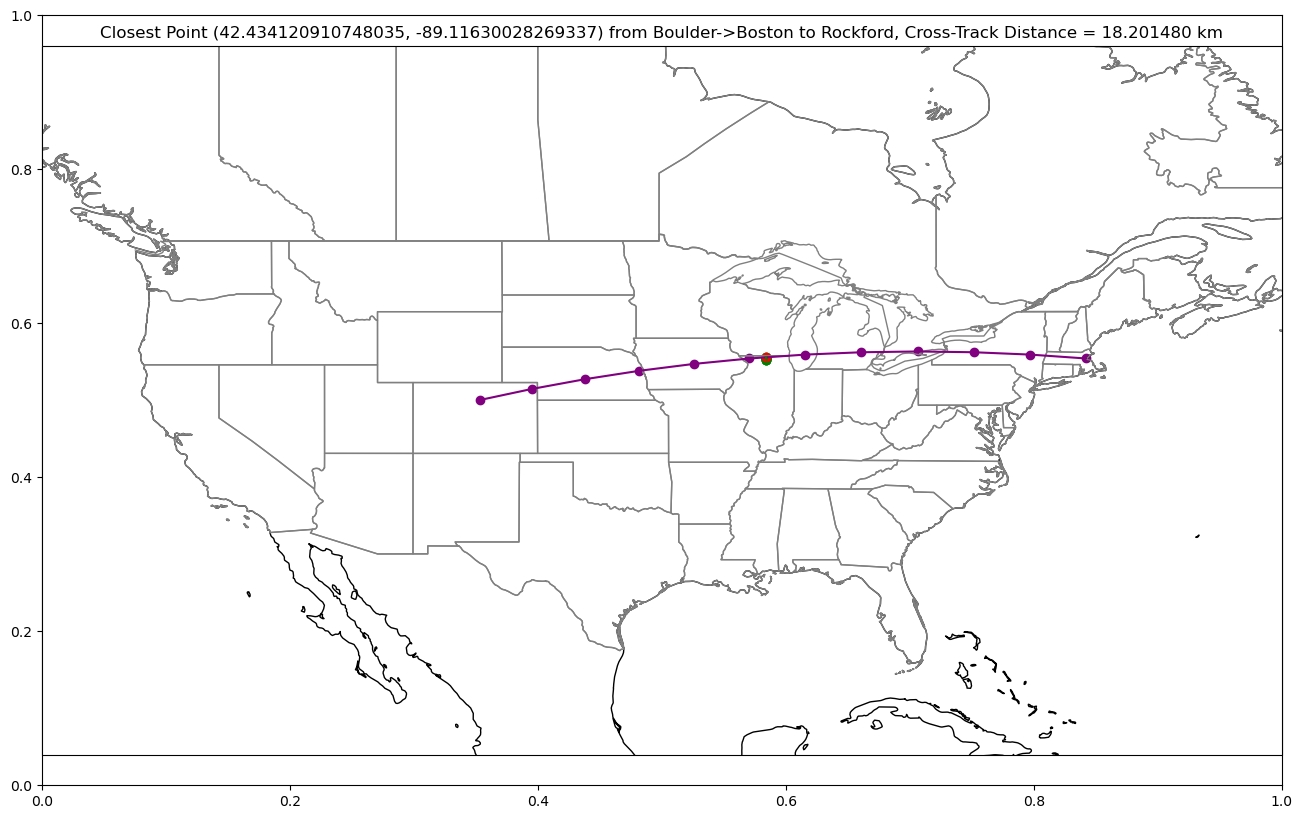
<Figure size 1600x1000 with 2 Axes>

Hard to see, right? Let’s zoom in:

plot_cross_track(start_point="boulder", end_point="boston", new_point="rockford", 
                 lon_west=-95, lon_east=-85,
                 lat_south=40, lat_north=45)
Cross Track Distance: 
18201.48035911659 meters (18.20148035911659 km)
Along Track Distance: 
1378654.5186233742 meters (1378.654518623374 km)

Closest Point To Point Along Great Circle Path:
(42.434120910748035, -89.11630028269337)

/home/runner/micromamba/envs/cookbook-gc/lib/python3.13/site-packages/cartopy/io/__init__.py:242: DownloadWarning: Downloading: https://naturalearth.s3.amazonaws.com/10m_physical/ne_10m_coastline.zip
  warnings.warn(f'Downloading: {url}', DownloadWarning)

/home/runner/micromamba/envs/cookbook-gc/lib/python3.13/site-packages/cartopy/io/__init__.py:242: DownloadWarning: Downloading: https://naturalearth.s3.amazonaws.com/10m_cultural/ne_10m_admin_0_boundary_lines_land.zip
  warnings.warn(f'Downloading: {url}', DownloadWarning)

/home/runner/micromamba/envs/cookbook-gc/lib/python3.13/site-packages/cartopy/io/__init__.py:242: DownloadWarning: Downloading: https://naturalearth.s3.amazonaws.com/10m_cultural/ne_10m_admin_1_states_provinces_lakes.zip
  warnings.warn(f'Downloading: {url}', DownloadWarning)
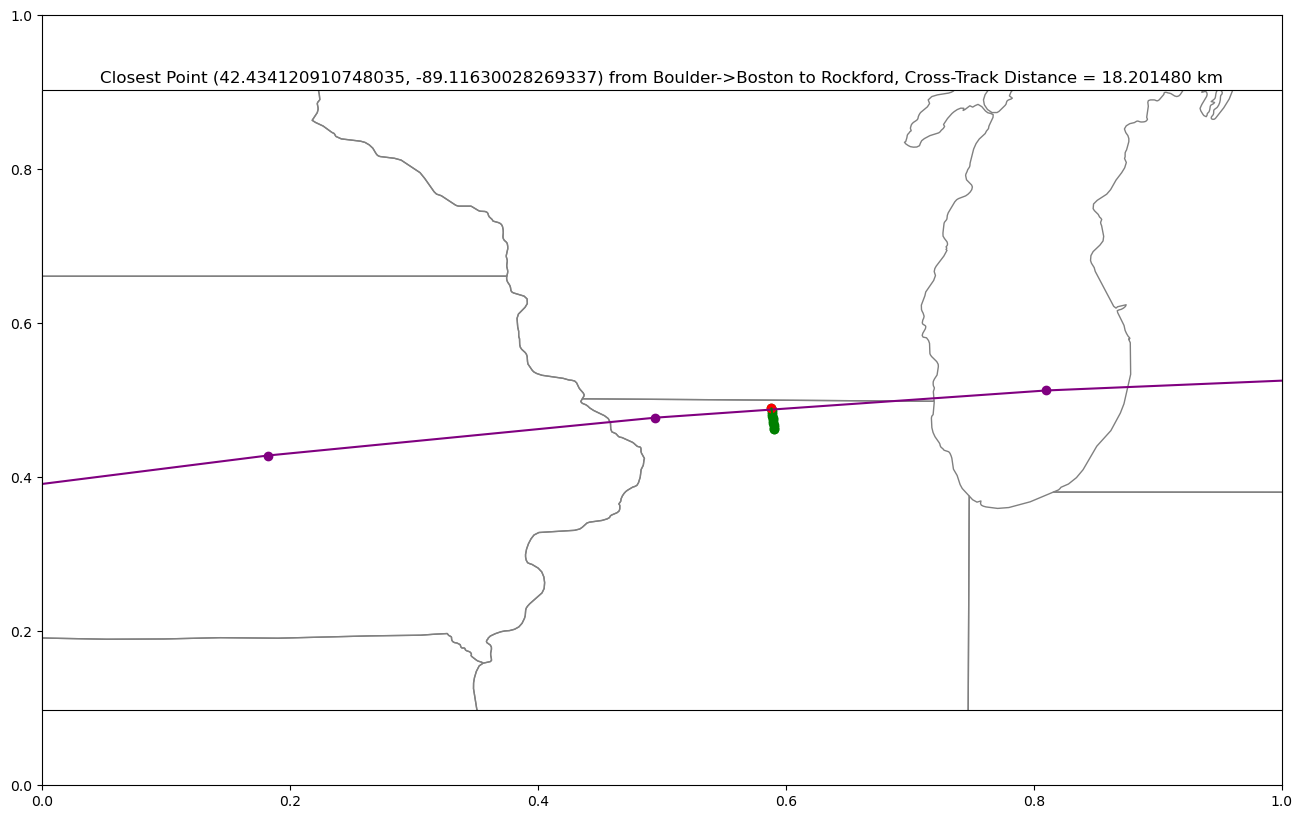
<Figure size 1600x1000 with 2 Axes>

18 km is far, but for the sake of clarity, maybe it serves our purposes as “on the arc”. If so, we can increase the tolerance of the function to about 18 km to encompass the town:

# increase tolerance to capture point
print("tolerance = 0")
print(is_point_on_arc("boulder", "boston", "rockford", tolerance=0))
print("\ntolerance >= cross-track distance")
print(is_point_on_arc("boulder", "boston", "rockford", tolerance=18202))
tolerance = 0
Cross-Track Distance = 18201.48035911659 meters
False

tolerance >= cross-track distance
Cross-Track Distance = 18201.48035911659 meters
True

(Optional) Additional Python Package: UXarray

UXarray acts as an Xarray extension for unstructured data (commonly used in climate and weather analysis). This includes multiple functions for working with great circles:

UXarray makes use of Cartesian coordinates and includes a very narrow built-in tolerance, but can be a simple solution if needed.

For example: Let’s check if a point lies on a great circle arc with UXarray (see example)

# Check if Boulder is on a great circle arc created by a point directly above (+latitude) and below (-latitude)

# Convert latitude and longitude points to Cartesian Points
def latlon_to_cart(lat, lon):
    from astropy.coordinates.representation import UnitSphericalRepresentation
    from astropy import units

    spherical_coords = UnitSphericalRepresentation(
        lat=lat * units.deg, lon=lon * units.deg
    )
    cart_coords = spherical_coords.to_cartesian()
    return np.array([cart_coords.x, cart_coords.y, cart_coords.z])


pt_within = latlon_to_cart(location_df.loc["boulder", "latitude"], location_df.loc["boulder", "longitude"]) # Boulder
vertex_a = latlon_to_cart(location_df.loc["boulder", "latitude"]+10, location_df.loc["boulder", "longitude"])  # Point exactly 10 degrees above Boulder
vertex_b = latlon_to_cart(location_df.loc["boulder", "latitude"]-10, location_df.loc["boulder", "longitude"])  # Point exactly 10 degrees below Boulder

# Determine if point lies along great circle arc
from uxarray.grid.arcs import point_within_gca

print(
    f"Boulder lies within the great circle arc = {point_within_gca(pt_within, vertex_a, vertex_b)}"
)
---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[15], line 20
     17 vertex_b = latlon_to_cart(location_df.loc["boulder", "latitude"]-10, location_df.loc["boulder", "longitude"])  # Point exactly 10 degrees below Boulder
     19 # Determine if point lies along great circle arc
---> 20 from uxarray.grid.arcs import point_within_gca
     22 print(
     23     f"Boulder lies within the great circle arc = {point_within_gca(pt_within, vertex_a, vertex_b)}"
     24 )

File ~/micromamba/envs/cookbook-gc/lib/python3.13/site-packages/uxarray/__init__.py:1
----> 1 from .grid import *
      2 from .dataset import *
      3 from .helpers import *

File ~/micromamba/envs/cookbook-gc/lib/python3.13/site-packages/uxarray/grid.py:13
     11 from ._shapefile import _read_shpfile
     12 from ._scrip import _read_scrip
---> 13 from .helpers import get_all_face_area_from_coords
     16 class Grid:
     17     """The Uxarray Grid object class that describes an unstructured grid.
     18 
     19     Examples
   (...)     28     >>> mesh.write("outfile.ug")
     29     """

File ~/micromamba/envs/cookbook-gc/lib/python3.13/site-packages/uxarray/helpers.py:5
      2 import xarray as xr
      3 from pathlib import PurePath
----> 5 from .get_quadratureDG import get_gauss_quadratureDG, get_tri_quadratureDG
      6 from numba import njit, config
      8 config.DISABLE_JIT = False

File ~/micromamba/envs/cookbook-gc/lib/python3.13/site-packages/uxarray/get_quadratureDG.py:2
      1 import numpy as np
----> 2 from numba import njit, config
      4 config.DISABLE_JIT = False
      7 @njit
      8 def get_gauss_quadratureDG(nCount):

ModuleNotFoundError: No module named 'numba'

Summary

In this notebook, we calculated and plotted the cross track and along track distance for points around a great circle arc

What’s next?

Next, we will determine when a great circle path crosses a given parallel and the maximum and minimum latitude coordinates of a great circle path.

Resources and references

Tutorials
Great Circle Arcs and Path
Tutorials
Great Circles and Parallels