Tiling of the sphere by spherical triangles

Spherical Polygons and Areas¶

Overview¶

In this notebook, we will calculate how to use spherical polygons on a unit sphere to determine areas and perimeters.

Calculate area and permieter of quadrilateral patch on a unit sphere
Determine if a given point is within a spherical polygon
Mean center of spherical polygon

Prerequisites¶

Concepts	Importance	Notes
Numpy	Necessary	Used to work with large arrays
Pandas	Necessary	Used to read in and organize data (in particular dataframes)
Intro to Cartopy	Helpful	Will be used for adding maps to plotting
Matplotlib	Helpful	Will be used for plotting

Time to learn: 20 minutes

Imports¶

Import Packages
Setup location dataframe with coordinates

import pandas as pd       # reading in data for location information from text file
import numpy as np        # working with arrays, vectors, cross/dot products, and radians

from pyproj import Geod   # working with the Earth as an ellipsod (WGS-84)

from shapely.geometry import Point
from shapely.geometry.polygon import Polygon

import matplotlib.pyplot as plt                        # plotting a graph
from cartopy import crs as ccrs, feature as cfeature   # plotting a world map

# Get all Coordinates for Locations
location_df = pd.read_csv("../location_full_coords.txt")
location_df = location_df.rename(columns=lambda x: x.strip()) # strip excess white space from column names and values
location_df.head()

location_df.index = location_df["name"]

Area and Perimeter of quadrilateral patch¶

We can make use of the pyproj Python package to calculate the area and perimeter of a patch formed by a list of latitude and longitude coordinates for an ellipsoid or a unit sphere.

def area_of_polygon_ellps(poly_pts=None):
    geod = Geod(ellps="WGS84")
    longitudes = [location_df.loc[pt, "longitude"] for pt in poly_pts]
    latitudes = [location_df.loc[pt, "latitude"] for pt in poly_pts]
    poly_area_m, poly_perimeter_m = geod.polygon_area_perimeter(longitudes, latitudes)
    return abs(poly_area_m) * 1e-6, poly_perimeter_m/1000 # km^2 and km

def area_of_polygon_unit_sphere(poly_pts=None):
    geod = Geod(ellps="sphere") # 'sphere': {'a': 6370997.0, 'b': 6370997.0, 'description': 'Normal Sphere (r=6370997)'
    longitudes = [location_df.loc[pt, "longitude"] for pt in poly_pts]
    latitudes = [location_df.loc[pt, "latitude"] for pt in poly_pts]
    poly_area_m, poly_perimeter_m = geod.polygon_area_perimeter(longitudes, latitudes)
    return abs(poly_area_m) * 1e-6, poly_perimeter_m/1000 # km^2 and km

Let’s compare how area and perimeter vary based on whether you use an ellpsoid like WGS-84 and a unit sphere. The changes will become more pronounced as you move further towards the poles.

area_ellps, perimeter_ellps = area_of_polygon_ellps(["boulder", "boston",
                                             "arecibo", "houston"])
area_us, perimeter_us = area_of_polygon_unit_sphere(["boulder", "boston",
                                             "arecibo", "houston"])
print(f"Area Ellipsoid   = {area_ellps} km^2")
print(f"Area Unit Sphere = {area_us} km^2")
print(f"Perimeter Ellipsoid = {perimeter_ellps} km")
print(f"Perimeter Unit SPhere = {perimeter_us} km")
print(f"Roughly {(area_ellps/509600000)*100:.2f}% of the Earth's Surface")
print(f"Roughly {(area_us/509600000)*100:.2f}% of the Earth's Surface")

Area Ellipsoid   = 5342585.6476998255 km^2
Area Unit Sphere = 5344606.94796931 km^2
Perimeter Ellipsoid = 10171.738963248145 km
Perimeter Unit SPhere = 10170.504728302833 km
Roughly 1.05% of the Earth's Surface
Roughly 1.05% of the Earth's Surface

Plot Area of Quadrilateral Patch¶

Let’s see what spherical polygons looks like on a world map!

def plot_area(pt_lst=None,
                   lon_west=-180, lon_east=180,
                   lat_south=-90, lat_north=90):
    # Set up world map plot
    fig = plt.subplots(figsize=(15, 10))
    projection_map = ccrs.PlateCarree()
    ax = plt.axes(projection=projection_map)
    ax.set_extent([lon_west, lon_east, lat_south, lat_north], crs=projection_map)
    ax.coastlines(color="black")
    ax.add_feature(cfeature.STATES, edgecolor="black")

   # plot points
    longitudes = [location_df.loc[x, "longitude"] for x in pt_lst] # longitude
    latitudes = [location_df.loc[y, "latitude"] for y in pt_lst] # latitude
    plt.scatter(longitudes, latitudes, s=100, c="red")
    plt.fill(longitudes, latitudes, alpha=0.5)

    # determine the area and perimeter
    area_ellps, perimeter_ellps = area_of_polygon_ellps(pt_lst)
    area_us, perimeter_us = area_of_polygon_unit_sphere(pt_lst)
    print(f"Ellipsoid Area   = {area_ellps} km^2")
    print(f"Unit Sphere Area = {area_us} km^2")
    plt.title(f"Roughly {(area_ellps/509600000)*100:.2f}% ({(area_us/509600000)*100:.2f}%) of the Earth's Surface")
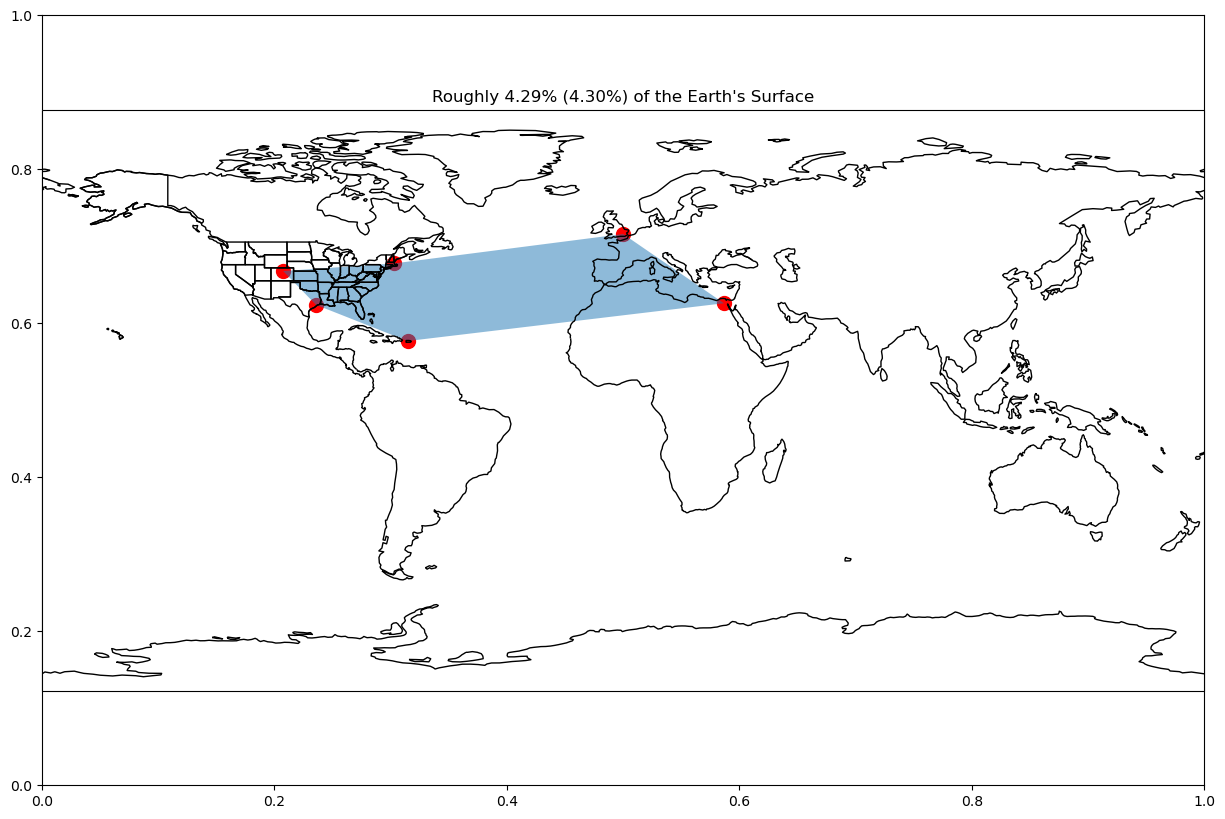
    plt.show()

plot_area(["boulder", "boston", "greenwich", "cairo", "arecibo", "houston"])

Ellipsoid Area   = 21872449.378265787 km^2
Unit Sphere Area = 21896220.663299154 km^2

/home/runner/micromamba/envs/cookbook-gc/lib/python3.13/site-packages/cartopy/io/__init__.py:242: DownloadWarning: Downloading: https://naturalearth.s3.amazonaws.com/110m_physical/ne_110m_coastline.zip
  warnings.warn(f'Downloading: {url}', DownloadWarning)

/home/runner/micromamba/envs/cookbook-gc/lib/python3.13/site-packages/cartopy/io/__init__.py:242: DownloadWarning: Downloading: https://naturalearth.s3.amazonaws.com/110m_cultural/ne_110m_admin_1_states_provinces_lakes.zip
  warnings.warn(f'Downloading: {url}', DownloadWarning)

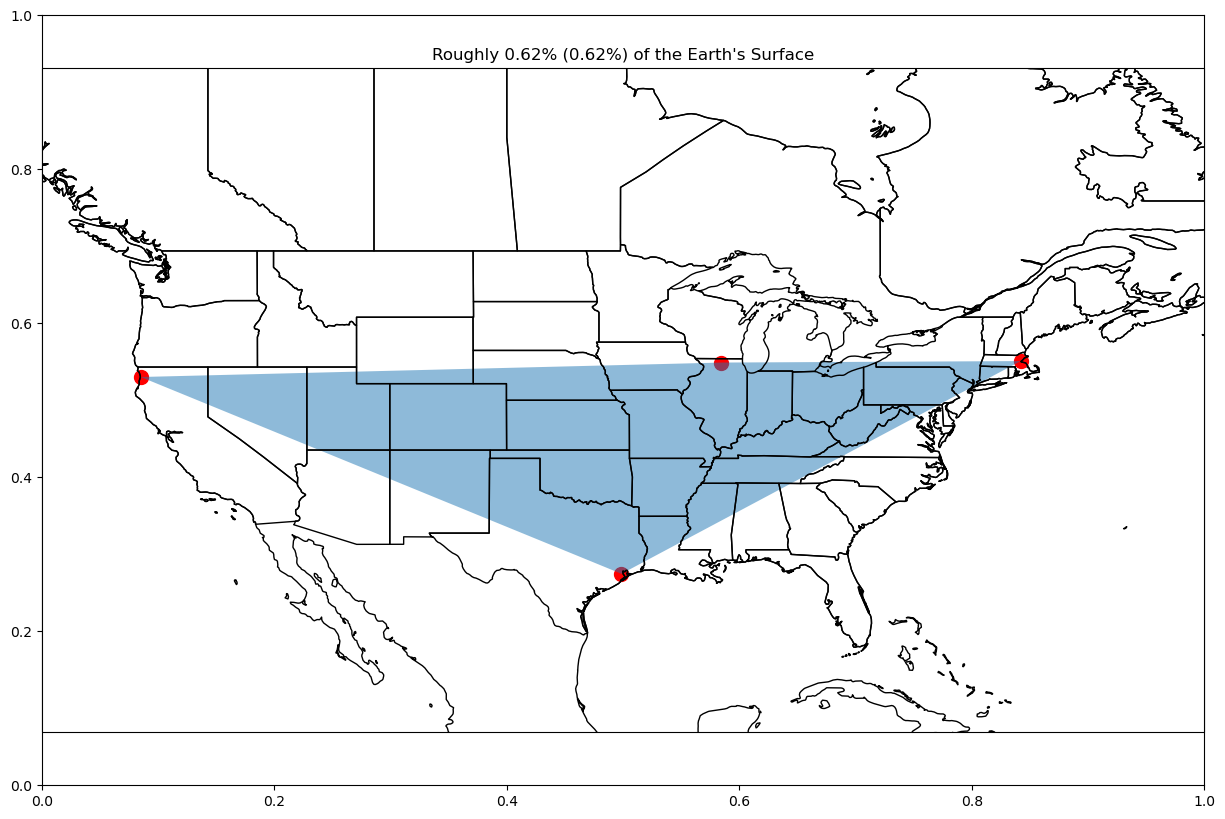
plot_area(["redwoods", "rockford", "boston", "houston",], -130, -60, 20, 60)

Ellipsoid Area   = 3150946.426714995 km^2
Unit Sphere Area = 3149017.3086414044 km^2

/home/runner/micromamba/envs/cookbook-gc/lib/python3.13/site-packages/cartopy/io/__init__.py:242: DownloadWarning: Downloading: https://naturalearth.s3.amazonaws.com/50m_cultural/ne_50m_admin_1_states_provinces_lakes.zip
  warnings.warn(f'Downloading: {url}', DownloadWarning)

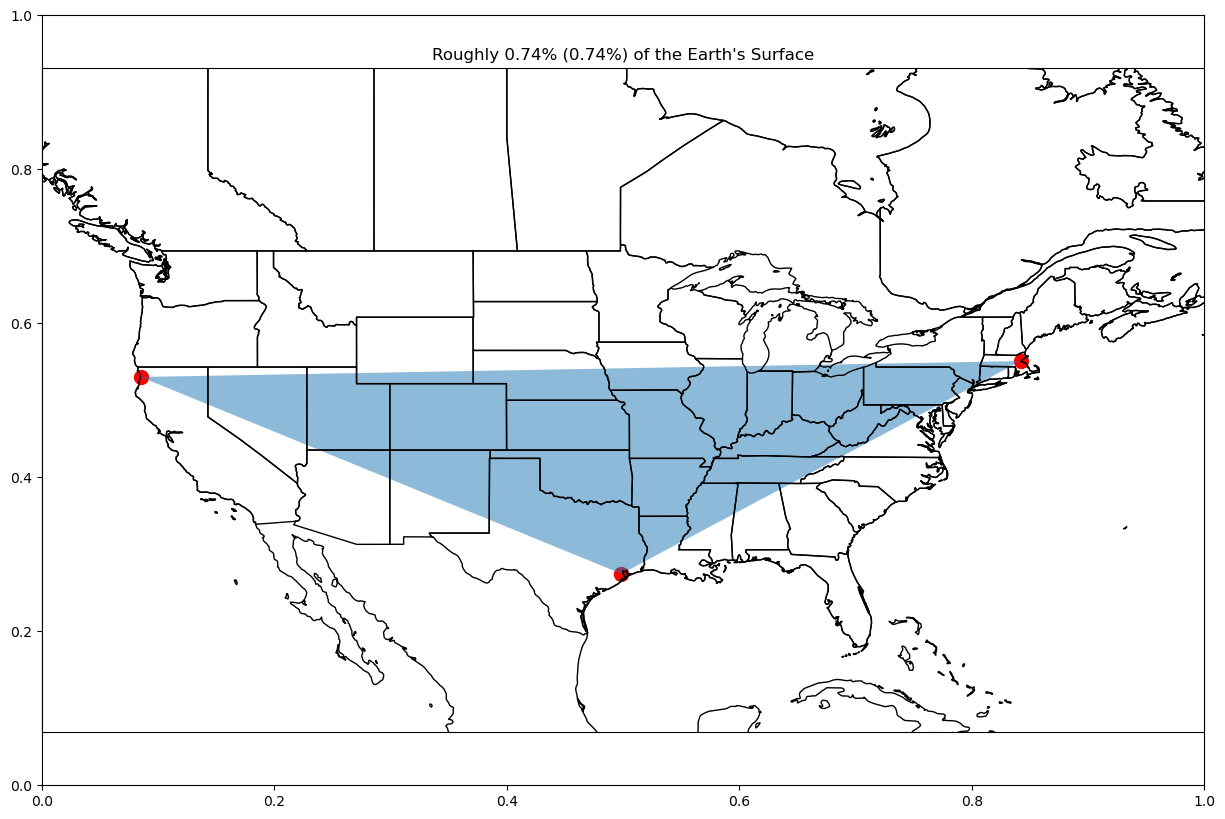
plot_area(["redwoods", "boston", "houston"], -130, -60, 20, 60)

Ellipsoid Area   = 3788155.432965353 km^2
Unit Sphere Area = 3782548.632737316 km^2

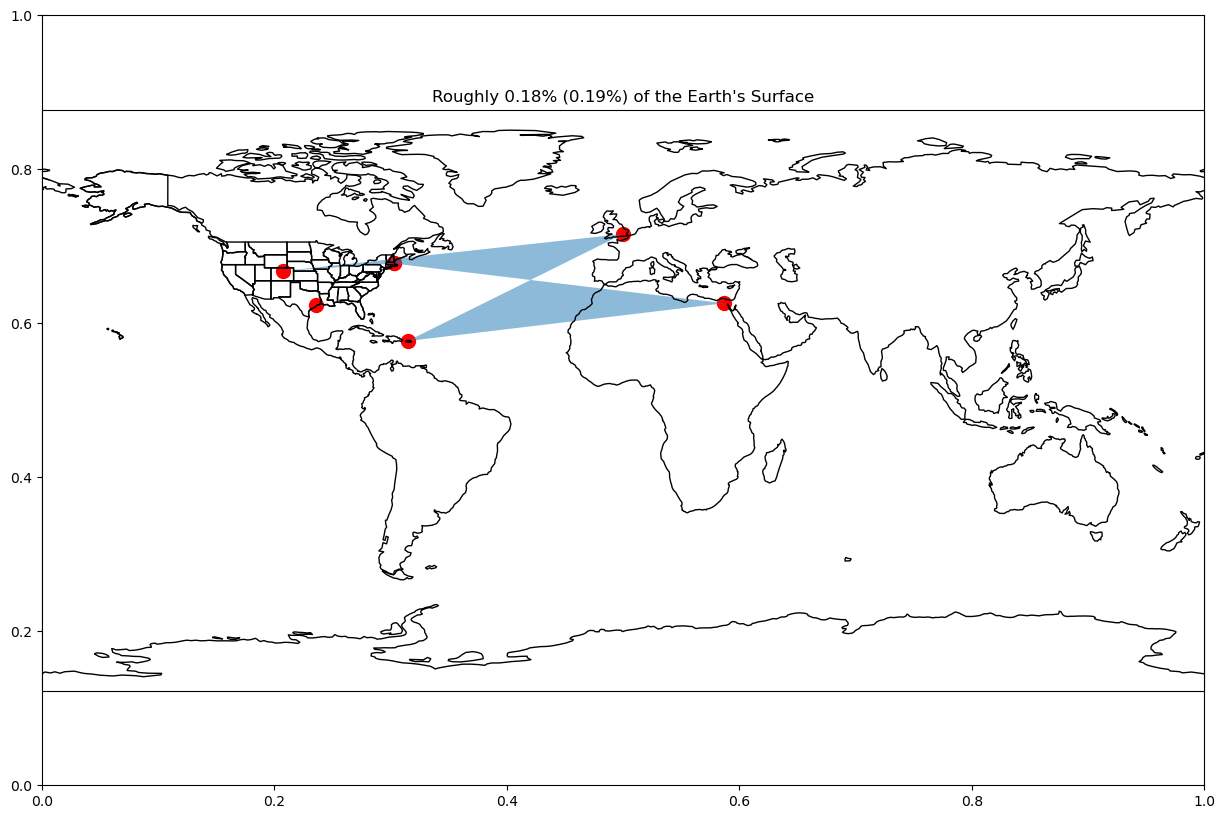
# For example: here is a list of unordered points
plot_area(["boulder", "boston", "houston", "boston", "cairo", "arecibo", "greenwich"])

Ellipsoid Area   = 914381.1786067598 km^2
Unit Sphere Area = 954445.989927043 km^2

Determine if a given point is within a spherical polygon¶

Now that we have a spherical polygon, how can be determine if a new point lies within the area of the polygon? The shapely Python package makes this quite easy, let’s give it a shot!

def polygon_contains_points(pt_lst=None, polygon_pts=None):
    longitudes = [location_df.loc[pt, "longitude"] for pt in polygon_pts]
    latitudes = [location_df.loc[pt, "latitude"] for pt in polygon_pts]
    lat_lon_coords = tuple(zip(longitudes, latitudes))
    # setup polygon
    polygon = Polygon(lat_lon_coords)
    # check if new point lies within the polygon
    contains = np.vectorize(lambda pt: polygon.contains(Point((location_df.loc[pt, "longitude"],
                                                               location_df.loc[pt, "latitude"]))))
    contained_by_polygon = contains(np.array(pt_lst))
    return contained_by_polygon

polygon_contains_points(["boulder"], ["redwoods", "boston", "houston"])

array([ True])

Plot and See if New Point within Polygon¶

On a map, it can be fairly intuitive to see if a point lies within a polygon or not. Let’s give it a shot!

def plot_polygon_pts(pt_lst=None, polygon_pts=None,
                   lon_west=-180, lon_east=180,
                   lat_south=-90, lat_north=90):
    # Set up world map plot
    fig = plt.subplots(figsize=(15, 10))
    projection_map = ccrs.PlateCarree()
    ax = plt.axes(projection=projection_map)
    ax.set_extent([lon_west, lon_east, lat_south, lat_north], crs=projection_map)
    ax.coastlines(color="black")
    ax.add_feature(cfeature.STATES, edgecolor="black")

    # plot polygon points
    longitudes = [location_df.loc[x, "longitude"] for x in polygon_pts] # longitude
    latitudes = [location_df.loc[y, "latitude"] for y in polygon_pts] # latitude
    plt.scatter(longitudes, latitudes, s=50, c="blue")
    plt.fill(longitudes, latitudes, alpha=0.5)

    # plot check points
    pt_lst = np.array(pt_lst)
    contains_pts = polygon_contains_points(pt_lst, polygon_pts)
    longitudes = [location_df.loc[x, "longitude"] for x in pt_lst[contains_pts]] # longitude
    latitudes = [location_df.loc[y, "latitude"] for y in pt_lst[contains_pts]] # latitude
    plt.scatter(longitudes, latitudes, s=100, c="green", label="Within Polygon")
    longitudes = [location_df.loc[x, "longitude"] for x in pt_lst[~contains_pts]] # longitude
    latitudes = [location_df.loc[y, "latitude"] for y in pt_lst[~contains_pts]] # latitude
    plt.scatter(longitudes, latitudes, s=100, c="red", label="Not within Polygon")

    plt.legend(loc="lower left")
    plt.title(f"Points contained within polygon = {pt_lst[contains_pts]}, not contained = {pt_lst[~contains_pts]}")
    plt.show()

polygon_contains_points(["boulder"], ["redwoods", "boston", "houston"])

array([ True])

plot_polygon_pts(["boulder"], ["redwoods", "boston", "houston"],
               -130, -60, 20, 60)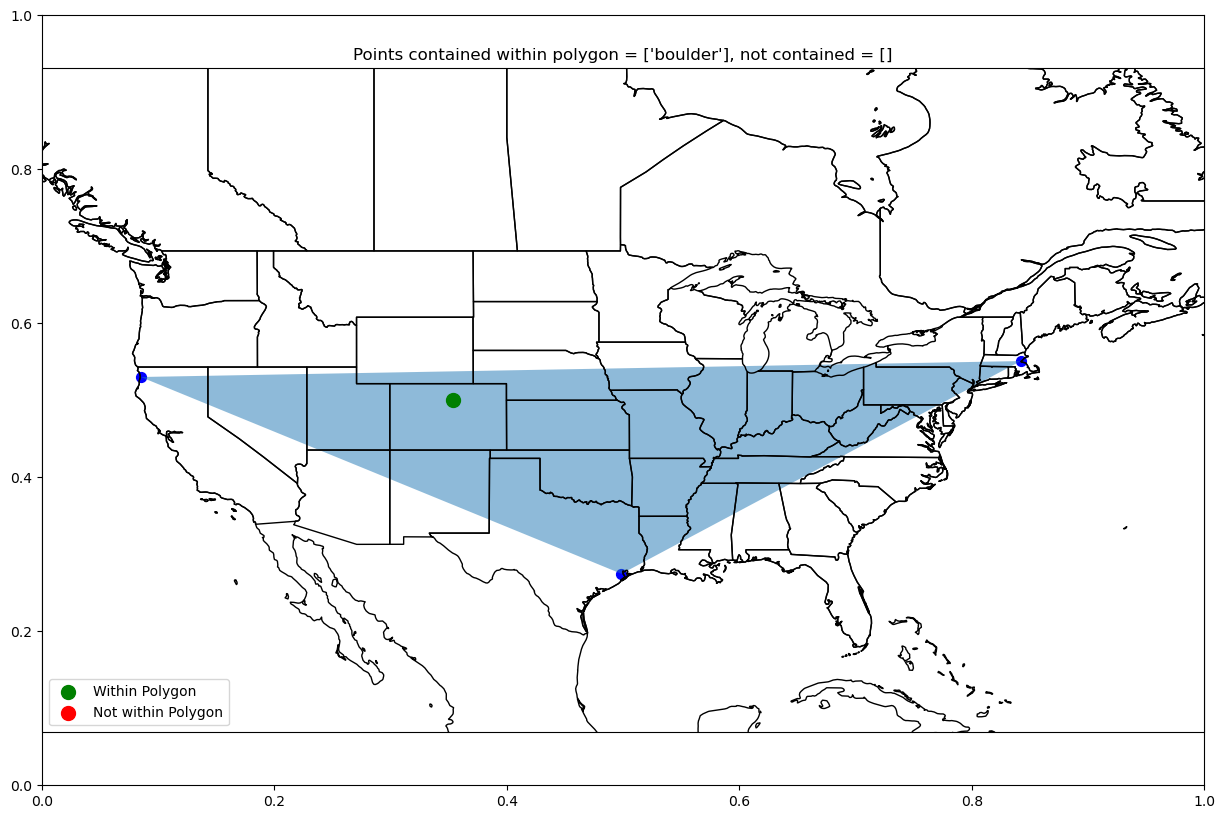

polygon_contains_points(["cape canaveral"], ["redwoods", "boston", "houston"])

array([False])

plot_polygon_pts(["cape canaveral"], ["redwoods", "boston", "houston"],
               -130, -60, 20, 60)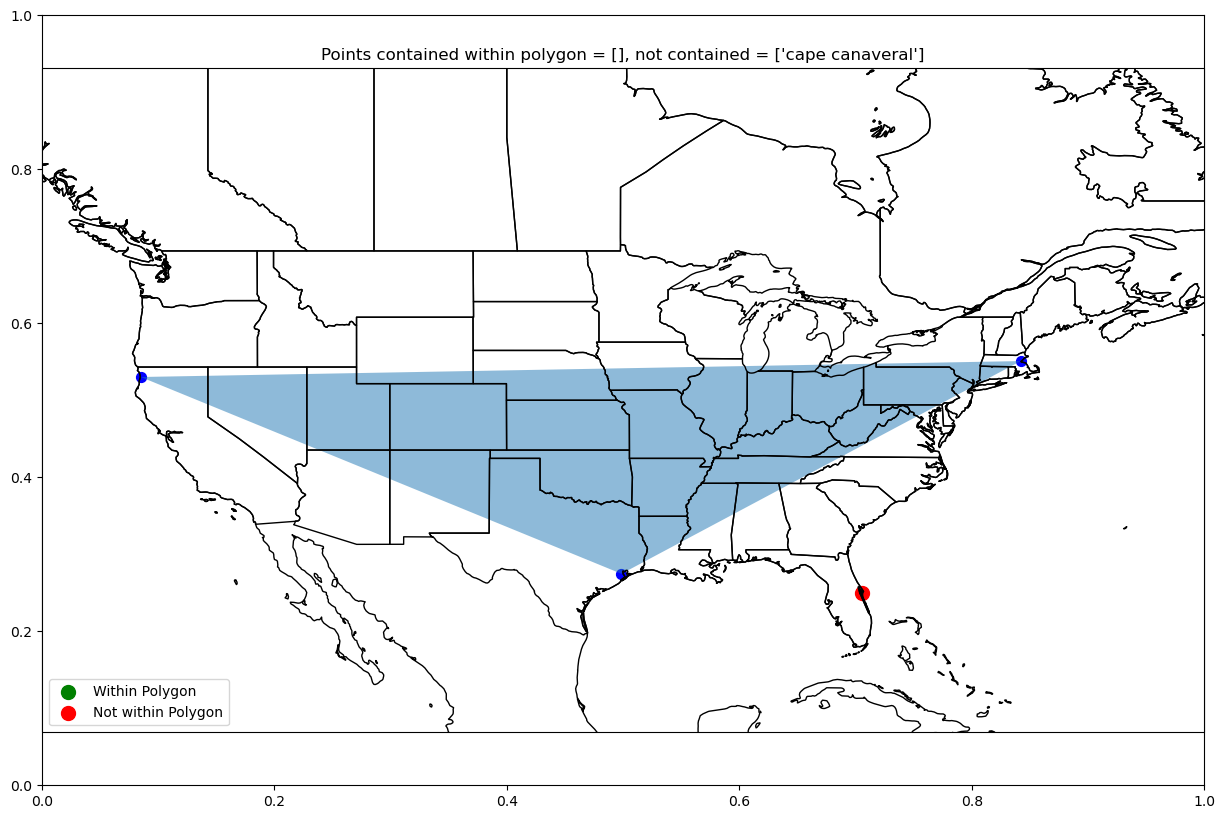

plot_polygon_pts(["boulder", "cape canaveral"], ["redwoods", "boston", "houston"],
               -130, -60, 20, 60)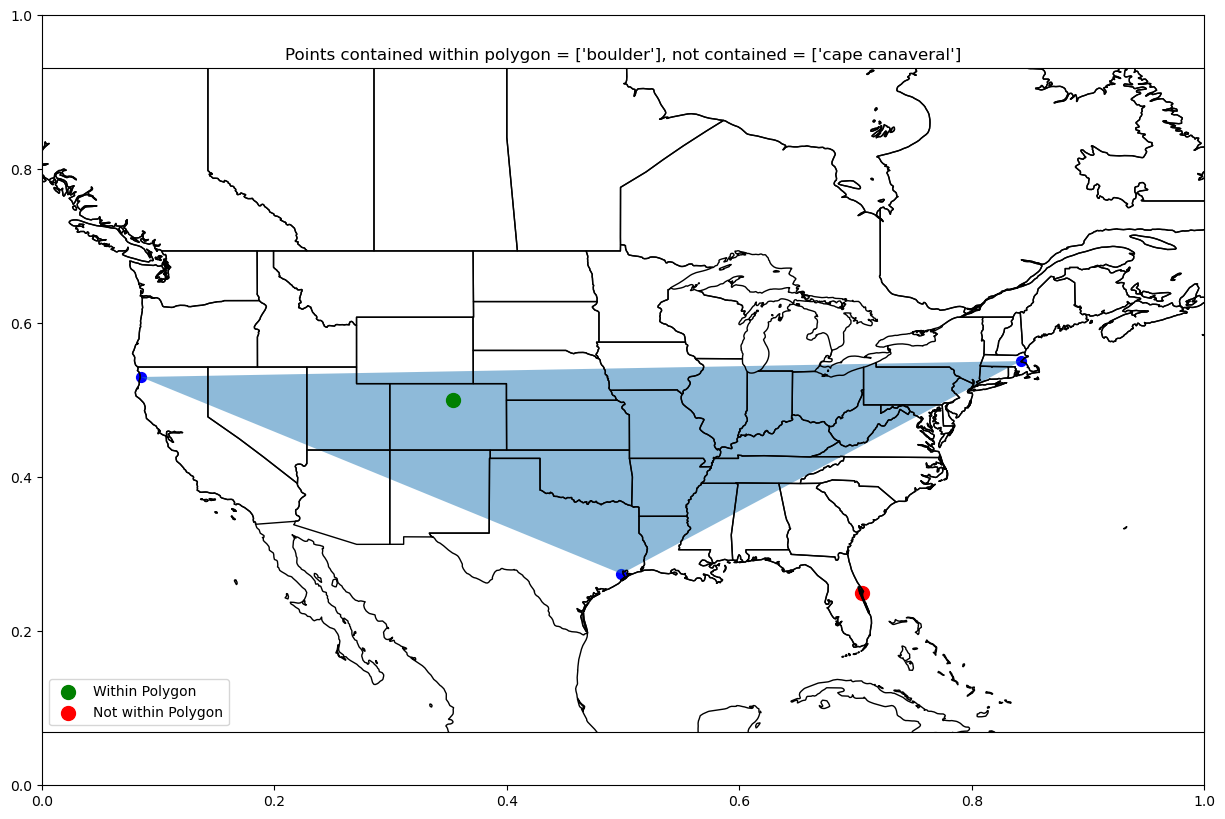

plot_polygon_pts(["boulder", "redwoods"], ["rockford", "boston", "cape canaveral"],
               -130, -60, 20, 60)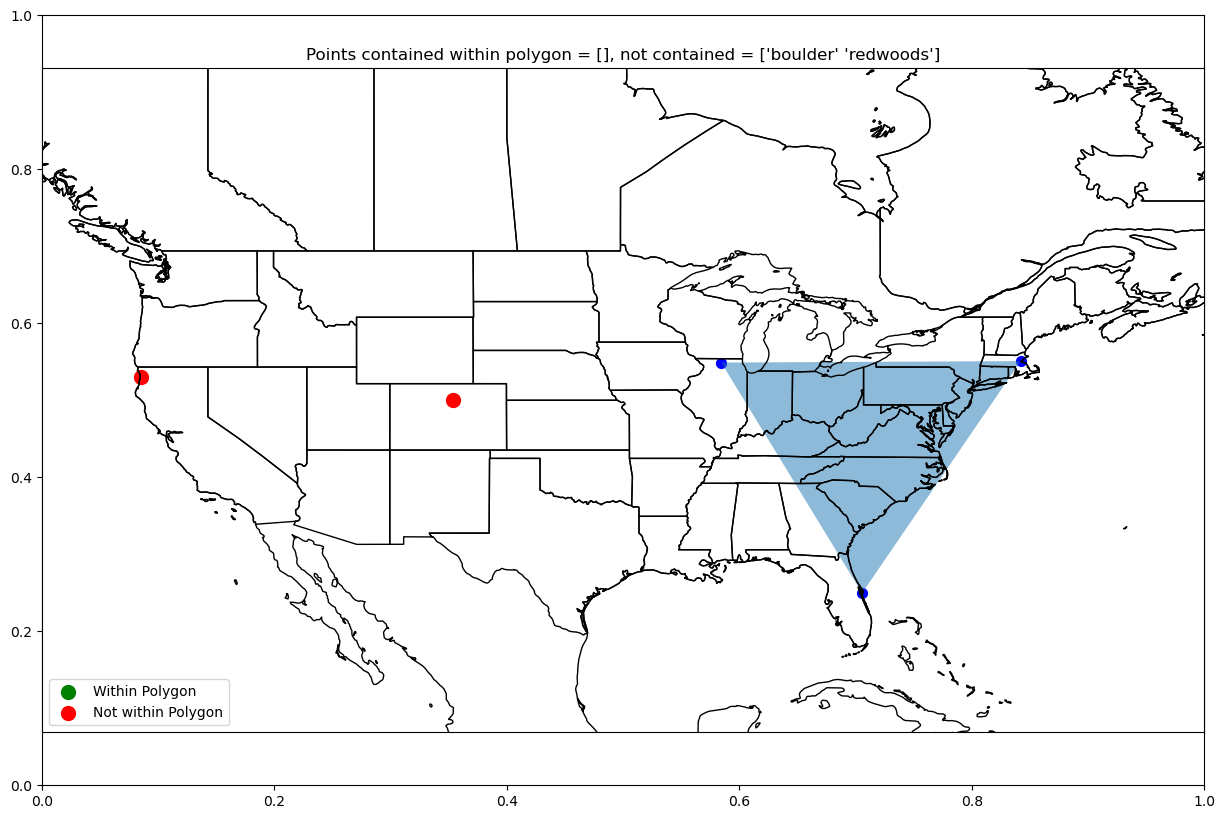

Mean center of spherical polygon¶

A spherical polygon can have a fairly regular shape, especially as more points are added. But it is fairly simple using the shapley Python package to determine the mean center.

def polygon_centroid(polygon_pts=None):
    longitudes = [location_df.loc[x, "longitude"] for x in polygon_pts]
    latitudes = [location_df.loc[y, "latitude"] for y in polygon_pts]
    lat_lon_coords = tuple(zip(longitudes, latitudes))
    polygon = Polygon(lat_lon_coords)
    return (polygon.centroid.y, polygon.centroid.x)

polygon_centroid(["boulder", "boston", "houston"])

(37.30896666666666, -90.47586666666665)

Plot Centroid¶

The center of a polygon can be fairly apparently on a map, let’s give it a look!

def plot_centroid(polygon_pts=None,
                   lon_west=-180, lon_east=180,
                   lat_south=-90, lat_north=90):
    # Set up world map plot
    fig = plt.subplots(figsize=(15, 10))
    projection_map = ccrs.PlateCarree()
    ax = plt.axes(projection=projection_map)
    ax.set_extent([lon_west, lon_east, lat_south, lat_north], crs=projection_map)
    ax.coastlines(color="black")
    ax.add_feature(cfeature.STATES, edgecolor="black")

   # plot polygon points
    longitudes = [location_df.loc[x, "longitude"] for x in polygon_pts] # longitude
    latitudes = [location_df.loc[y, "latitude"] for y in polygon_pts] # latitude
    plt.scatter(longitudes, latitudes, s=50, c="blue")
    plt.fill(longitudes, latitudes, alpha=0.5)

    # plot check point
    centeroid = polygon_centroid(polygon_pts)
    plt.scatter(centeroid[1], centeroid[0], s=100, c="red")
    plt.title(f"Centroid = {centeroid}")
    plt.show()

plot_centroid(["boulder", "boston", "houston"],
               -130, -60, 20, 60)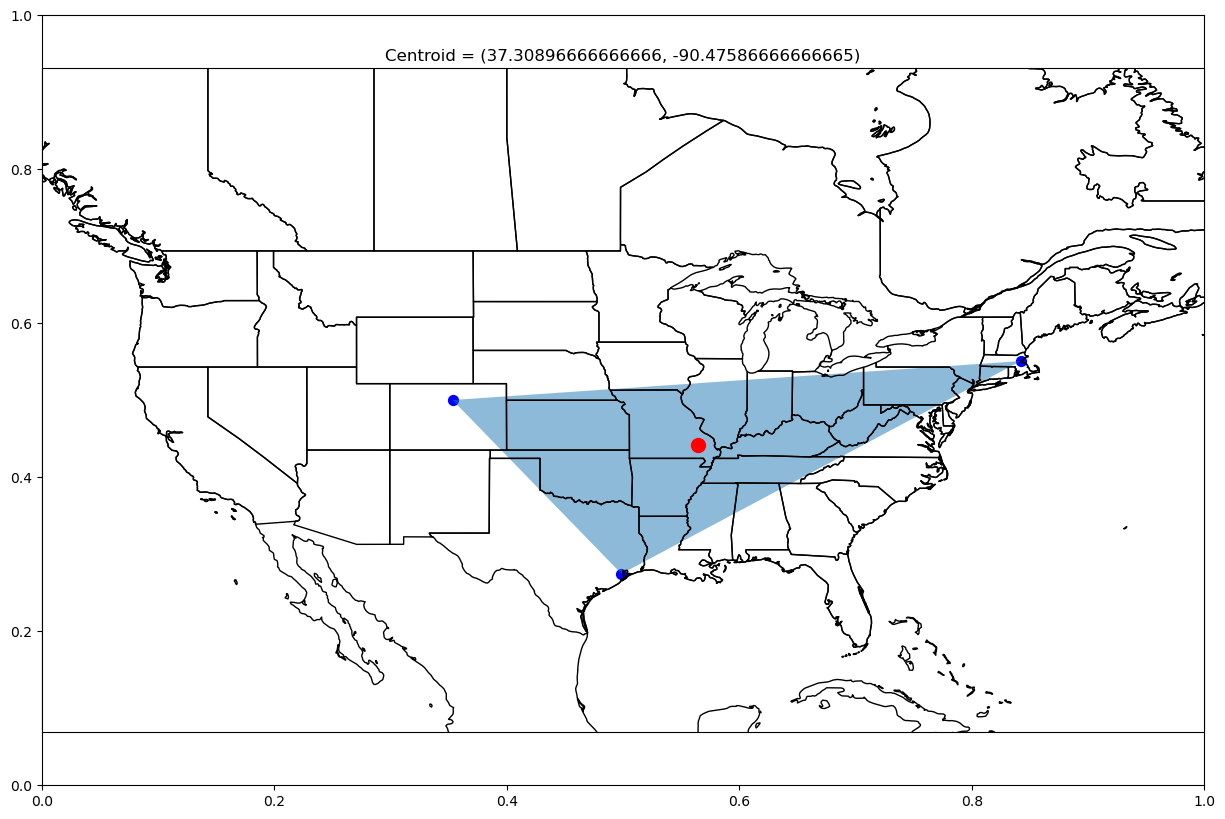

plot_centroid(["redwoods", "boulder", "cape canaveral", "houston"],
               -130, -60, 20, 60)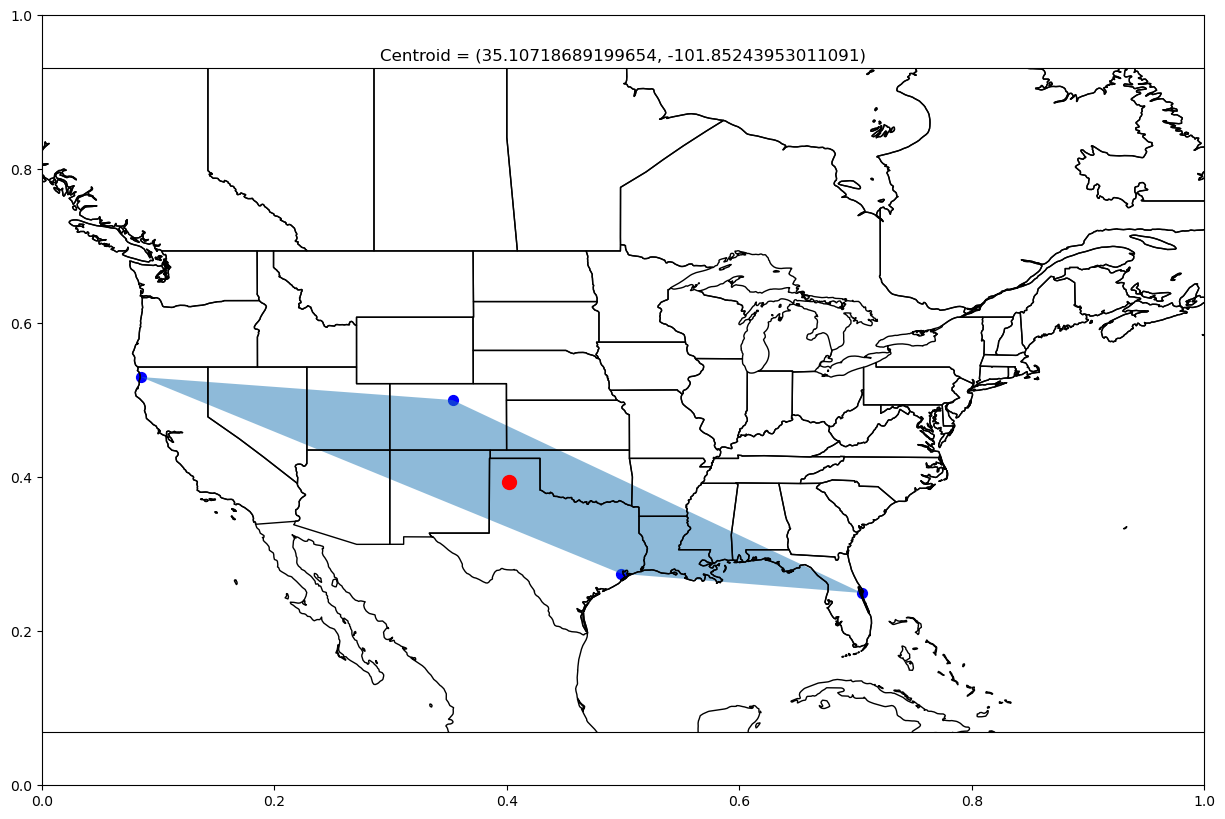

Summary¶

This notebook covers working with spherical polygons to determine the ordering of coordinates, center of polygons, and whether or not a point lies within a spherical polygon

Resources and references¶

Tutorials

Angles and Great Circles