Illustrating the spherical triangles forming the pentagramma mirificum on Wikipedia

Angles and Great Circles¶

Overview¶

Multiple great circle paths will always intersection at some point along the globe, and at these points, they form internal angles.

Determine the acute and obtuse angle formed by two great circle paths
Determine the directed angle formed by two great circle paths based on an intersection point

Prerequisites¶

Concepts	Importance	Notes
Numpy	Necessary	Used to work with large arrays
Pandas	Necessary	Used to read in and organize data (in particular dataframes)
Intro to Cartopy	Helpful	Will be used for adding maps to plotting
Matplotlib	Helpful	Will be used for plotting

Time to learn: 30 minutes

Imports¶

Import Packages
Setup location dataframe with coordinates

import pandas as pd       # reading in data for location information from text file
import numpy as np        # working with arrays, vectors, cross/dot products, and radians

from pyproj import Geod   # working with the Earth as an ellipsod (WGS-84)
import geopy.distance     # working with the Earth as an ellipsod

import matplotlib.pyplot as plt                        # plotting a graph
from cartopy import crs as ccrs, feature as cfeature   # plotting a world map

# Get all Coordinates for Locations
location_df = pd.read_csv("../location_full_coords.txt")
location_df = location_df.rename(columns=lambda x: x.strip()) # strip excess white space from column names and values
location_df.head()

location_df.index = location_df["name"]

Determine the acute and obtuse angle formed by two great circle paths¶

At an intersection point, two great circle paths will form both an acute and obtuse angle.

def angle_between_arcs(start_gc1=None, end_gc1=None,
                       start_gc2=None, end_gc2=None):
    # get normal of planes containing great circles
    normal_one = np.cross([location_df.loc[start_gc1, "cart_x"],
                           location_df.loc[start_gc1, "cart_y"],
                           location_df.loc[start_gc1, "cart_z"]],
                          [location_df.loc[end_gc1, "cart_x"],
                           location_df.loc[end_gc1, "cart_y"],
                           location_df.loc[end_gc1,"cart_z"]])
    normal_two = np.cross([location_df.loc[start_gc2, "cart_x"],
                           location_df.loc[start_gc2, "cart_y"],
                           location_df.loc[start_gc2, "cart_z"]],
                          [location_df.loc[end_gc2, "cart_x"],
                           location_df.loc[end_gc2, "cart_y"],
                           location_df.loc[end_gc2,"cart_z"]])

    # dot product to obtain the angle between the normal planes
    angle_between_planes = np.dot(normal_one, normal_two)

    # divide by the magnitude of the vectors, inverse of cos to find angle
    angle = np.arccos(np.dot(normal_one, normal_two) / 
                    (np.linalg.norm(normal_one) * np.linalg.norm(normal_two)))
    obtuse_acute_angle = (float(np.rad2deg(angle)), float(((360-(2*np.rad2deg(angle)))/2)))
    obtuse_angle = np.max(obtuse_acute_angle)

    print(f"Acute Angle  = {np.min(obtuse_acute_angle)} degrees")
    print(f"Obtuse Angle = {np.max(obtuse_acute_angle)} degrees")
    return obtuse_acute_angle

angle_between_arcs("boulder", "boston", "johannesburg", "reykjavík")

Acute Angle  = 30.646334650419192 degrees
Obtuse Angle = 149.3536653495808 degrees

(149.3536653495808, 30.646334650419192)

Determine the directed angle formed by two great circle paths based on an intersection point¶

Overview of Directed Angles¶

Most angles are undirected angles, where the configuration of the sides that form the angle are not important. A directed angle is useful when the configuration and ordering of the sides is important.

For example, three points A, B, and C, define the sides of an angle (A->B and A->C) where A is the intersection point of the two arcs AB and AC. An undirected angle will return an unsigned value. However, a directed angle returns a signed angle, where it is:

Positive if C is to the left of the great circle arc AB
Negative if C is to the right of the great circle arc AB

So, a directed positive angle is counterclockwise, while a negative angle is clockwise.

def directed_angle(b_coords=None, c_coords=None, a_coords=None):
    # determine cartesian_coordinates from intersect points
    earth_radius = 6378137  # meters
    latitude = np.deg2rad(a_coords[0])
    longitude = np.deg2rad(a_coords[1])
    cart_x = earth_radius * np.cos(latitude) * np.cos(longitude)
    cart_y = earth_radius * np.cos(latitude) * np.sin(longitude)
    cart_z = earth_radius * np.sin(latitude)

    # get normal of planes containing great circles
    normal_one = np.cross([cart_x,
                           cart_y,
                           cart_z],
                          [location_df.loc[b_coords, "cart_x"],
                           location_df.loc[b_coords, "cart_y"],
                           location_df.loc[b_coords, "cart_z"]])
    normal_two = np.cross([cart_x,
                           cart_y,
                           cart_z],
                          [location_df.loc[c_coords, "cart_x"],
                           location_df.loc[c_coords, "cart_y"],
                           location_df.loc[c_coords, "cart_z"]])
    # dot product to obtain the angle between the normal planes
    angle_between_planes = np.dot(normal_one, normal_two)
    # divide by the magnitude of the vectors, inverse of cos to find angle
    angle = np.arccos(np.dot(normal_one, normal_two) / 
                    (np.linalg.norm(normal_one) * np.linalg.norm(normal_two)))
    angle = np.rad2deg(angle)

    # take the cross product of two vectors A->B and A->C
    v_ab = np.array([[cart_x,
                    cart_y,
                    cart_z],
                    [location_df.loc[b_coords, "cart_x"],
                     location_df.loc[b_coords, "cart_y"],
                     location_df.loc[b_coords, "cart_z"]]])
    v_ac = np.array([[cart_x,
                    cart_y,
                    cart_z],
                    [location_df.loc[c_coords, "cart_x"],
                     location_df.loc[c_coords, "cart_y"],
                     location_df.loc[c_coords, "cart_z"]]])

    cross_prod = np.cross(v_ab, v_ac)

    # inverse of the sign of the cross product
    sign_angle = -1*np.sign(cross_prod[1][-1]) * angle
    return float(sign_angle)

Calculate Intersection Point Between Two Great Circle Paths¶

# See previous notebook to see how this function is defined

def intersection_of_gc(start_gc1=None, end_gc1=None,
                      start_gc2=None, end_gc2=None):
    # get normal of planes containing great circles

    # cross product of vectors
    normal_one = np.cross([location_df.loc[start_gc1, "cart_x"],
                           location_df.loc[start_gc1, "cart_y"],
                           location_df.loc[start_gc1, "cart_z"]],
                          [location_df.loc[end_gc1, "cart_x"],
                           location_df.loc[end_gc1, "cart_y"],
                           location_df.loc[end_gc1, "cart_z"]])
    normal_two = np.cross([location_df.loc[start_gc2, "cart_x"],
                           location_df.loc[start_gc2, "cart_y"],
                           location_df.loc[start_gc2, "cart_z"]],
                          [location_df.loc[end_gc2, "cart_x"],
                           location_df.loc[end_gc2, "cart_y"],
                           location_df.loc[end_gc2, "cart_z"]])

    # intersection of planes, normal to the poles of each plane
    line_of_intersection = np.cross(normal_one, normal_two)

    # intersection points (one on each side of the earth)
    x1 = line_of_intersection /  np.sqrt(line_of_intersection[0]**2 + line_of_intersection[1]**2 + line_of_intersection[2]**2) 
    x2 = -x1
    lat1 = np.rad2deg(np.arctan2(x1[2], np.sqrt(pow(x1[0],2)+pow(x1[1],2))))
    lon1 = np.rad2deg(np.arctan2(x1[1], x1[0]))
    lat2 = np.rad2deg(np.arctan2(x2[2], np.sqrt(pow(x2[0],2)+pow(x2[1],2))))
    lon2 = np.rad2deg(np.arctan2(x2[1], x2[0]))
    return [(float(lat1), float(lon1)), (float(lat2), float(lon2))]

intersect_pts = intersection_of_gc("boulder", "boston", "johannesburg", "reykjavík")
print(f"Intersection points between great circle arc 1 (Boulder -> Boston) and 2 (Johannesburg -> Reykjavík): \n{intersect_pts}")

Intersection points between great circle arc 1 (Boulder -> Boston) and 2 (Johannesburg -> Reykjavík): 
[(-12.168951714418165, 22.965145304597574), (12.168951714418165, -157.03485469540243)]

# Arcs defined as A->B and A->C where A is the intersection
directed_angle(a_coords=intersect_pts[0],
               b_coords="boulder",
               c_coords="reykjavík")

-30.64633465041918

# Arcs defined as A->B and A->C where A is the intersection
directed_angle(a_coords=intersect_pts[-1],
               b_coords="boulder",
               c_coords="reykjavík")

-30.646334650419192

Plot Directed Angle¶

A negative directed angle is clockwise, while a positive directed angle is counterclockwise. This can be easier to understand when plotted. The directed angle is measured counterclockwise from the first coordinate.

Directed Angle Definition: "Given any two non-parallel lines l and m, we define the directed angle to be measured of the angle starting from l and ending at m, measured counterclockwise. So the angle lm and the angle ml are 180 degrees

See more: Directed Angles

# See previous section for more information

# Generate Latitude Coordinates based on Longitude Coordinates
def generate_latitude_along_gc(start_lat=None, start_lon=None,
                               end_lat=None, end_lon=None,
                               number_of_lon_pts=360):
    lon1 = np.deg2rad(start_lon)
    lat1 = np.deg2rad(start_lat)
    lon2 = np.deg2rad(end_lon)
    lat2 = np.deg2rad(end_lat)

    # Verify not meridian (longitude passes through the poles)
    if np.sin(lon1 - lon2) == 0:
        print("Invalid inputs: start/end points are meridians")
        # plotting meridians at 0 longitude through all latitudes
        meridian_lat = np.arange(-90, 90, 180/len(longitude_lst)) # split in n number
        meridians = []
        for lat in meridian_lat:
            meridians.append((lat, 0))
        return meridians

    # verify not anitpodal (diametrically opposite, points)
    if lat1 + lat2 == 0 and abs(lon1-lon2) == np.pi:
        print("Invalid inputs: start/end points are antipodal")
        return []

    # note: can be expanded to handle input of np arrays by filter out antipodal/merdiain points

    # generate n total number of longitude points along the great circle
    # https://github.com/rspatial/geosphere/blob/master/R/greatCircle.R#L18C3-L18C7
    gc_lon_lst = []
    for lon in range(1, number_of_lon_pts+1):
        new_lon = (lon  * (360/number_of_lon_pts) - 180)
        gc_lon_lst.append(np.deg2rad(new_lon))

    # Intermediate points on a great circle: https://edwilliams.org/avform147.htm"
    gc_lat_lon = []
    for gc_lon in gc_lon_lst:
        num = np.sin(lat1)*np.cos(lat2)*np.sin(gc_lon-lon2)-np.sin(lat2)*np.cos(lat1)*np.sin(gc_lon-lon1)
        den = np.cos(lat1)*np.cos(lat2)*np.sin(lon1-lon2)
        new_lat = np.arctan(num/den)
        gc_lat_lon.append((np.rad2deg(new_lat), np.rad2deg(gc_lon)))
    return gc_lat_lon

def interpolate_points_along_gc(lat_start=None, lon_start=None,
                                lat_end=None, lon_end=None,
                                distance_between_points_meter=0): 
    geodesic = Geod(ellps="WGS84")
    
    lat_lon_points = [(lat_start, lon_start)]
    
    # move to next point when distance between points is less than the equal distance
    move_to_next_point = True
    while(move_to_next_point):
        forward_bearing, _, distance_meters = geodesic.inv(lon_start,
                                                            lat_start, 
                                                            lon_end,
                                                            lat_end)
        if distance_meters < distance_between_points_meter:
            # ends before overshooting
            move_to_next_point = False
        else:
            start_point = geopy.Point(lat_start, lon_start)
            distance_to_move = geopy.distance.distance(
                            kilometers=distance_between_points_meter /
                            1000)  # distance to move towards the next point
            final_position = distance_to_move.destination(
                            start_point, bearing=forward_bearing)
            lat_lon_points.append((final_position.latitude, final_position.longitude))
            # new starting position is newly found end position
            lon_start, lat_start = final_position.longitude, final_position.latitude
    lat_lon_points.append((lat_end, lon_end))
    return lat_lon_points

def arc_points(start_lat=None, start_lon=None,
               end_lat=None, end_lon=None,
               n_total_points=10):

    geodesic = Geod(ellps="WGS84")

    _, _, distance_meter =  geodesic.inv(start_lon,
                                        start_lat,
                                        end_lon,
                                        end_lat)
        
    distance_between_points_meter = distance_meter / (n_total_points + 1)

    
    points_along_arc = interpolate_points_along_gc(start_lat, start_lon,
                                                   end_lat, end_lon,
                                                    distance_between_points_meter)
    return points_along_arc

def plot_gc_directed_angle(a_coords=None, b_coords=None,c_coords=None,
                           angle=None,
                           lon_west=-180, lon_east=180,
                           lat_south=-90, lat_north=90):
    # A = intersect point
    # A->B and A->C where C is the angle to determine sign

    # Set up world map plot
    fig = plt.subplots(figsize=(15, 10))
    projection_map = ccrs.PlateCarree()
    ax = plt.axes(projection=projection_map)
    ax.set_extent([lon_west, lon_east, lat_south, lat_north], crs=projection_map)
    ax.coastlines(color="black")
    ax.add_feature(cfeature.STATES, edgecolor="black")

    # Plot Great Circle Path
    gc_one_lat_pts = generate_latitude_along_gc(start_lat=a_coords[0],
                                                start_lon=a_coords[1],
                                                end_lat=location_df.loc[b_coords, "latitude"],
                                                end_lon=location_df.loc[b_coords, "longitude"])
    longitudes = [x[1] for x in gc_one_lat_pts] # longitude
    latitudes = [x[0] for x in gc_one_lat_pts] # latitude
    plt.plot(longitudes, latitudes)
    gc_two_lat_pts =  generate_latitude_along_gc(start_lat=a_coords[0],
                                                start_lon=a_coords[1],
                                                end_lat=location_df.loc[c_coords, "latitude"],
                                                end_lon=location_df.loc[c_coords, "longitude"])
    longitudes = [x[1] for x in gc_two_lat_pts] # longitude
    latitudes = [x[0] for x in gc_two_lat_pts] # latitude
    plt.plot(longitudes, latitudes)

    # Plot Great Circle Arc
    gc_one_arc_pts = arc_points(start_lat=a_coords[0],
                               start_lon=a_coords[1],
                               end_lat=location_df.loc[b_coords, "latitude"],
                               end_lon=location_df.loc[b_coords, "longitude"])
    longitudes = [x[1] for x in gc_one_arc_pts] # longitude
    latitudes = [x[0] for x in gc_one_arc_pts] # latitude
    plt.plot(longitudes, latitudes, c="pink")
    gc_two_arc_pts = arc_points(start_lat=a_coords[0],
                               start_lon=a_coords[1],
                               end_lat=location_df.loc[c_coords, "latitude"],
                               end_lon=location_df.loc[c_coords, "longitude"])
    longitudes = [x[1] for x in gc_two_arc_pts] # longitude
    latitudes = [x[0] for x in gc_two_arc_pts] # latitude
    plt.plot(longitudes, latitudes, c="green")

    # plot A, B, C points in different colors
    fz = 30
    offset = 3
    plt.scatter(a_coords[1], a_coords[0], s=100, c="red", label="A")
    ax.annotate("A", (a_coords[1]+offset, a_coords[0]+offset), fontsize=fz)
    plt.scatter(location_df.loc[b_coords, "longitude"],
               location_df.loc[b_coords, "latitude"],
                s=100, c="blue", label="B")
    ax.annotate("B", (location_df.loc[b_coords, "longitude"]-(4*offset),
                      location_df.loc[b_coords, "latitude"]-offset),
                        fontsize=fz)
    plt.scatter(location_df.loc[c_coords, "longitude"],
                location_df.loc[c_coords, "latitude"], 
                s=100, c="cyan", label="C")
    ax.annotate("C", (location_df.loc[c_coords, "longitude"]+offset,
                      location_df.loc[c_coords, "latitude"]+offset),
                        fontsize=fz)
    ax.quiver(location_df.loc[b_coords, "longitude"],
              location_df.loc[b_coords, "latitude"], 
              (location_df.loc[c_coords, "longitude"]-location_df.loc[b_coords, "longitude"]), 
              (location_df.loc[c_coords, "latitude"]-location_df.loc[b_coords, "latitude"]), 
              angles='xy', scale_units='xy', scale=1)    
    
    if angle > 0: 
        sign = "Counterclockwise"
    if angle < 0: 
        sign = "Clockwise"
    if angle == 0:
        sign = "Colinear"
    plt.title(f"Direction = {sign}, {angle}")
    plt.legend()
    plt.show()

# Arcs defined as A->B and A->C where A is the intersection
intersect_pts = intersection_of_gc("boulder", "boston", "reykjavík", "johannesburg")

direct_angle = directed_angle(a_coords=intersect_pts[0],
                              b_coords="boulder",
                              c_coords="reykjavík")

plot_gc_directed_angle(a_coords=intersect_pts[0],
                       b_coords="boulder",
                       c_coords="reykjavík",
                       angle=direct_angle)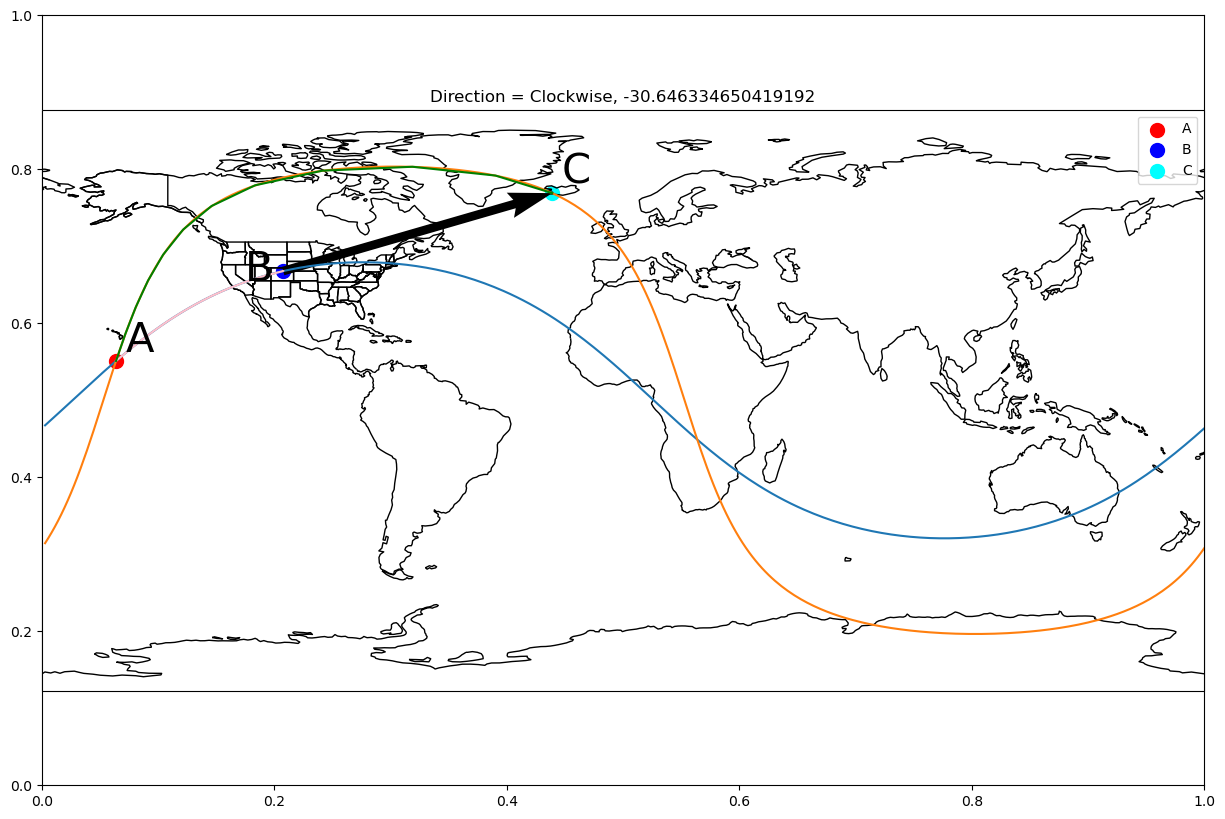

# Arcs defined as A->B and A->C where A is the intersection
intersect_pts = intersection_of_gc("boulder", "boston", "reykjavík", "johannesburg")

direct_angle = directed_angle(a_coords=intersect_pts[-1],
                              b_coords="boulder",
                              c_coords="reykjavík")

plot_gc_directed_angle(a_coords=intersect_pts[-1],
                       b_coords="boulder",
                       c_coords="reykjavík",
                       angle=direct_angle)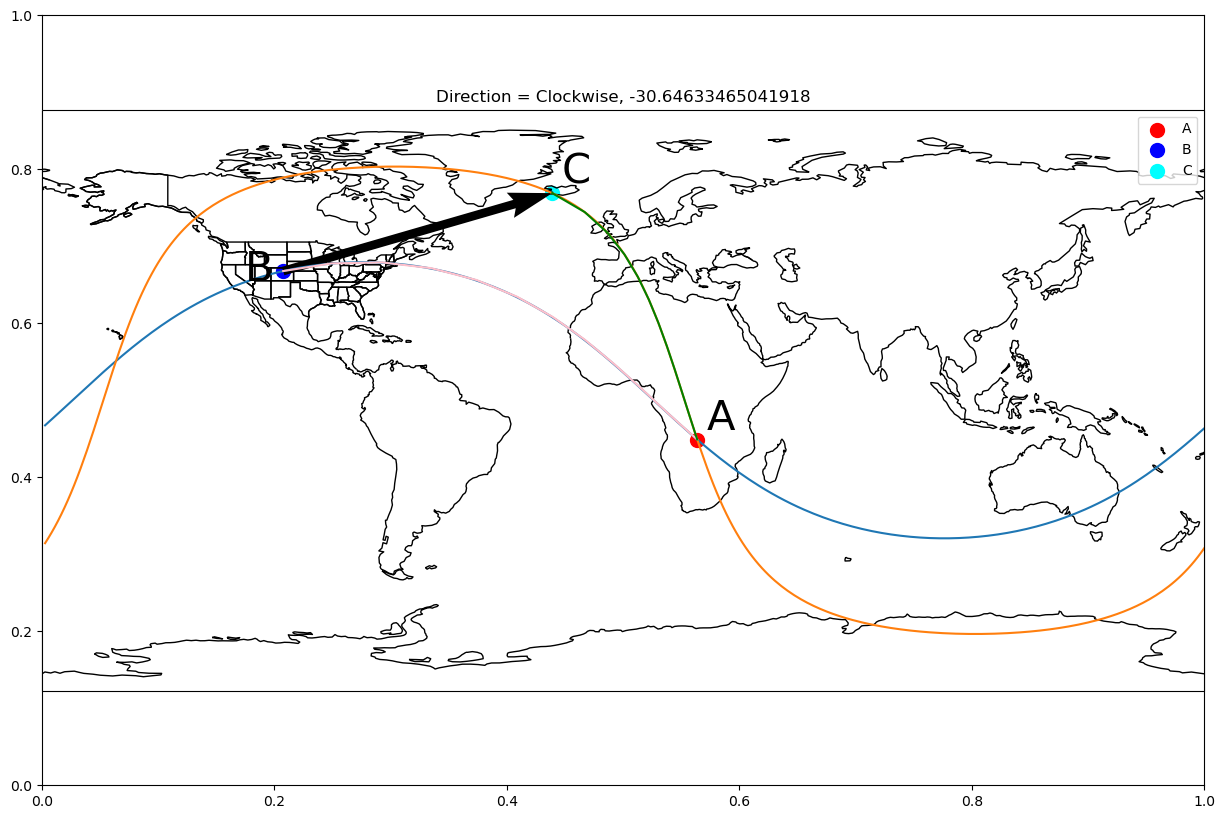

# Arcs defined as A->B and A->C where A is the intersection
intersect_pts = intersection_of_gc("zambezi", "boston", "greenwich", "johannesburg")

direct_angle = directed_angle(a_coords=intersect_pts[0],
                              b_coords="zambezi",
                              c_coords="greenwich")

plot_gc_directed_angle(a_coords=intersect_pts[0],
                       b_coords="zambezi",
                       c_coords="reykjavík",
                       angle=direct_angle)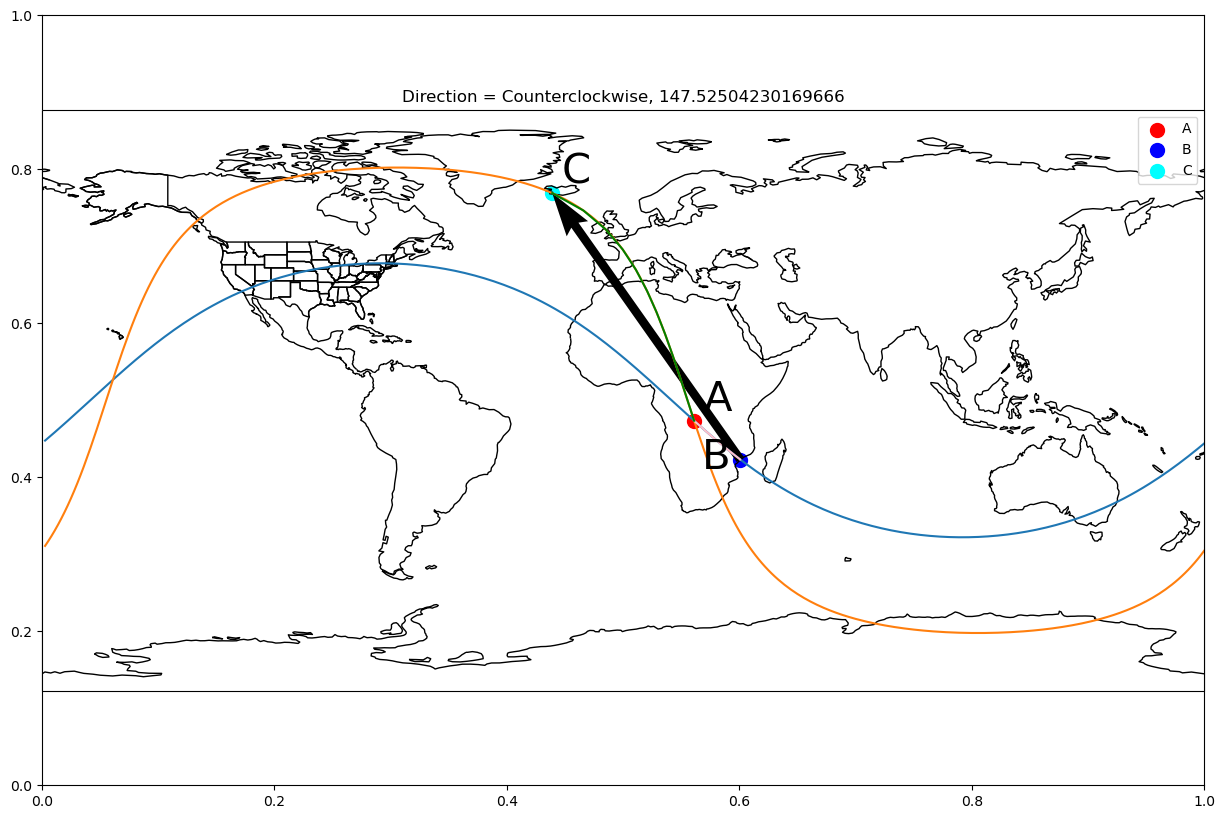

# Arcs defined as A->B and A->C where A is the intersection
intersect_pts = intersection_of_gc("zambezi", "boston", "greenwich", "johannesburg")

direct_angle = directed_angle(a_coords=intersect_pts[-1],
                              b_coords="zambezi",
                              c_coords="greenwich")

plot_gc_directed_angle(a_coords=intersect_pts[-1],
                       b_coords="zambezi",
                       c_coords="reykjavík",
                       angle=direct_angle)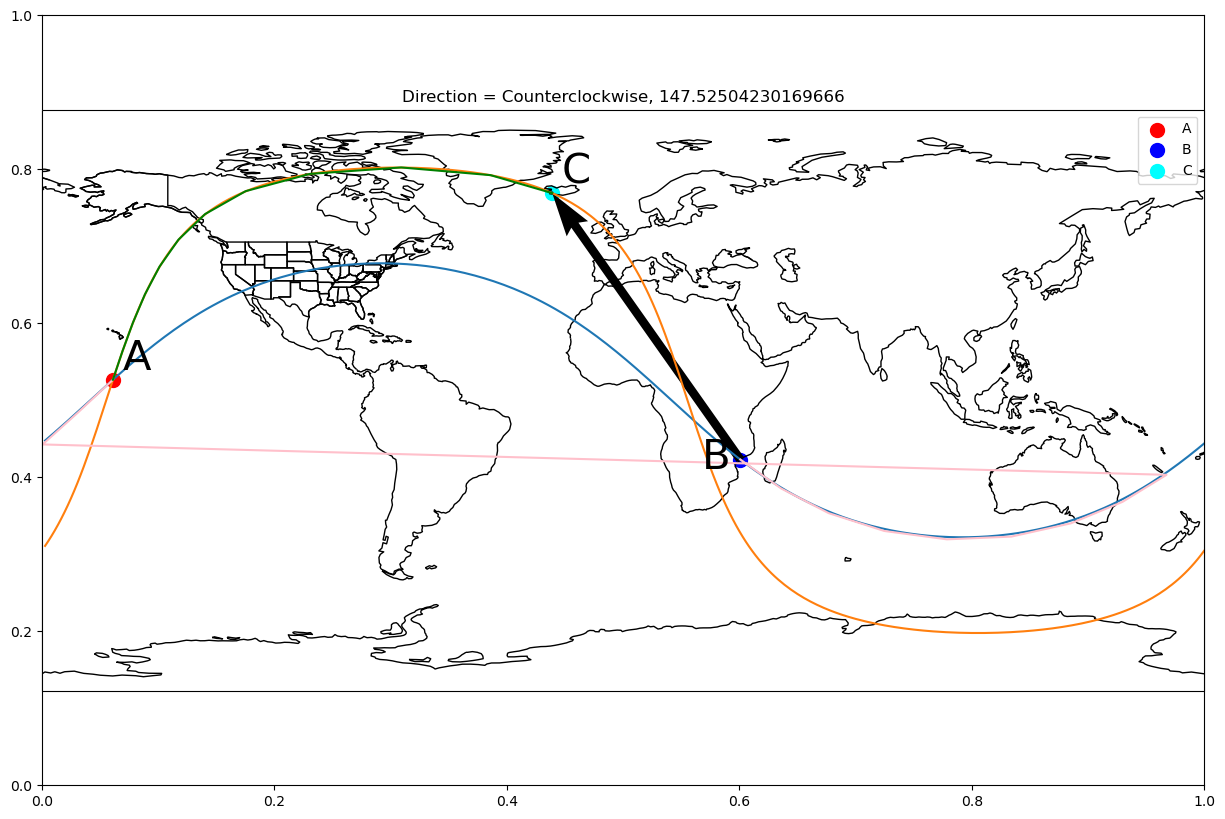

Summary¶

In this notebook, we determined how to find the angles and directed angle formed by the intersection of two great circle paths.

What’s next?¶

Up next, we will cover how to calculate spherical polygons and the area of spherical polygons.

Angles and Great Circles