Speckle Statistics

This notebook will provide an empirical demonstration of speckle - how it originates, how it visually and statistically looks like, and some of the most common approaches to filter it.

Speckle is defined as a kind of noise that affects all radar images. Given the multiple scattering contributions originating from the various elementary objects present within a resolution cell, the resulting backscatter signal can be described as a random constructive and destructive interference of wavelets. As a consequence, speckle is the reason why a granular pattern normally affects SAR images, making it more challenging to interpret and analyze them.

Credits: ESRI

import json
from functools import partial

import holoviews as hv
import intake
import matplotlib.pyplot as plt
import numpy as np
from holoviews.streams import RangeXY
from scipy.ndimage import uniform_filter

hv.extension("bokeh")

ⓘ

Let’s make an example of a cornfield (with a typical backscattering value of about -10 dB). According to the following equation:

\[ \sigma^0 = \frac{1}{\text{area}} \sum_{n \in \text{area}} \sigma_n \]

We should ideally have a uniform discrete sigma naught \(\sigma^0\) value, given that the cornfield pixel is the only individual contributor.

However, since we already learned from the previous notebooks that a pixel’s ground size can be in the order of tens of meters (i.e., 10 meters for Sentinel-1), we can imagine that different distributed targets in the scene contribute to the global backscattered information.

Let´s replicate this behavior with an ideal uniform area constituted by 100 pixels and then by adding 30% of speckle.

ideal_backscatter = -10  # in dB, a typical value for cornfields
width = 12
size = (width, width)
ideal_data = np.full(size, ideal_backscatter)
ideal_data_linear = 10 ** (
    ideal_data / 10
)  # Convert dB to linear scale for speckle addition

speckle_fraction = 0.3
num_speckled_pixels = int(
    size[0] * size[1] * speckle_fraction
)  # Rayleigh speckle noise
speckled_indices = np.random.choice(
    width * width, num_speckled_pixels, replace=False
)  # random indices for speckle

# Initialize speckled data as the same as the ideal data
speckled_data_linear = ideal_data_linear.copy()

speckle_noise = np.random.gumbel(scale=1.0, size=num_speckled_pixels)
speckled_data_linear.ravel()[
    speckled_indices
] *= speckle_noise  # Add speckle to the selected pixels

ideal_data_dB = 10 * np.log10(ideal_data_linear)
speckled_data_dB = 10 * np.log10(speckled_data_linear)
plt.figure(figsize=(16, 10))

# Ideal data
plt.subplot(2, 2, 1)
plt.imshow(ideal_data_dB, cmap="gray", vmin=-20, vmax=0)
plt.title("Ideal Backscatter (Cornfield)")
plt.colorbar(label="Backscatter (dB)")

# Speckled data
plt.subplot(2, 2, 2)
plt.imshow(speckled_data_dB, cmap="gray", vmin=-20, vmax=0)
plt.title(f"Speckled Backscatter ({int(speckle_fraction * 100)}% of Pixels)")
plt.colorbar(label="Backscatter (dB)")

bins = 25
hist_ideal, bins_ideal = np.histogram(ideal_data_dB.ravel(), bins=bins, range=(-20, 0))
hist_speckled, bins_speckled = np.histogram(
    speckled_data_dB.ravel(), bins=bins, range=(-20, 0)
)
max_freq = max(
    hist_ideal.max(), hist_speckled.max()
)  # maximum frequency for normalization

# Histogram for ideal data
plt.subplot(2, 2, 3)
plt.hist(ideal_data_dB.ravel(), bins=bins, range=(-20, 0), color="gray", alpha=0.7)
plt.ylim(0, max_freq)
plt.title("Histogram of Ideal Backscatter")
plt.xlabel("Backscatter (dB)")
plt.ylabel("Frequency")

# Histogram for speckled data
plt.subplot(2, 2, 4)
plt.hist(speckled_data_dB.ravel(), bins=bins, range=(-20, 0), color="gray", alpha=0.7)
plt.ylim(0, max_freq)
plt.title(f"Histogram of Speckled Backscatter ({int(speckle_fraction * 100)}%)")
plt.xlabel("Backscatter (dB)")
plt.ylabel("Frequency")

plt.tight_layout()

/tmp/ipykernel_4627/3459812397.py:26: RuntimeWarning: invalid value encountered in log10
  speckled_data_dB = 10 * np.log10(speckled_data_linear)

../../../../_images/6c120001341b92b2dc0662496b6a2ecf6c21ff15950b94b74716589af32045bc.png

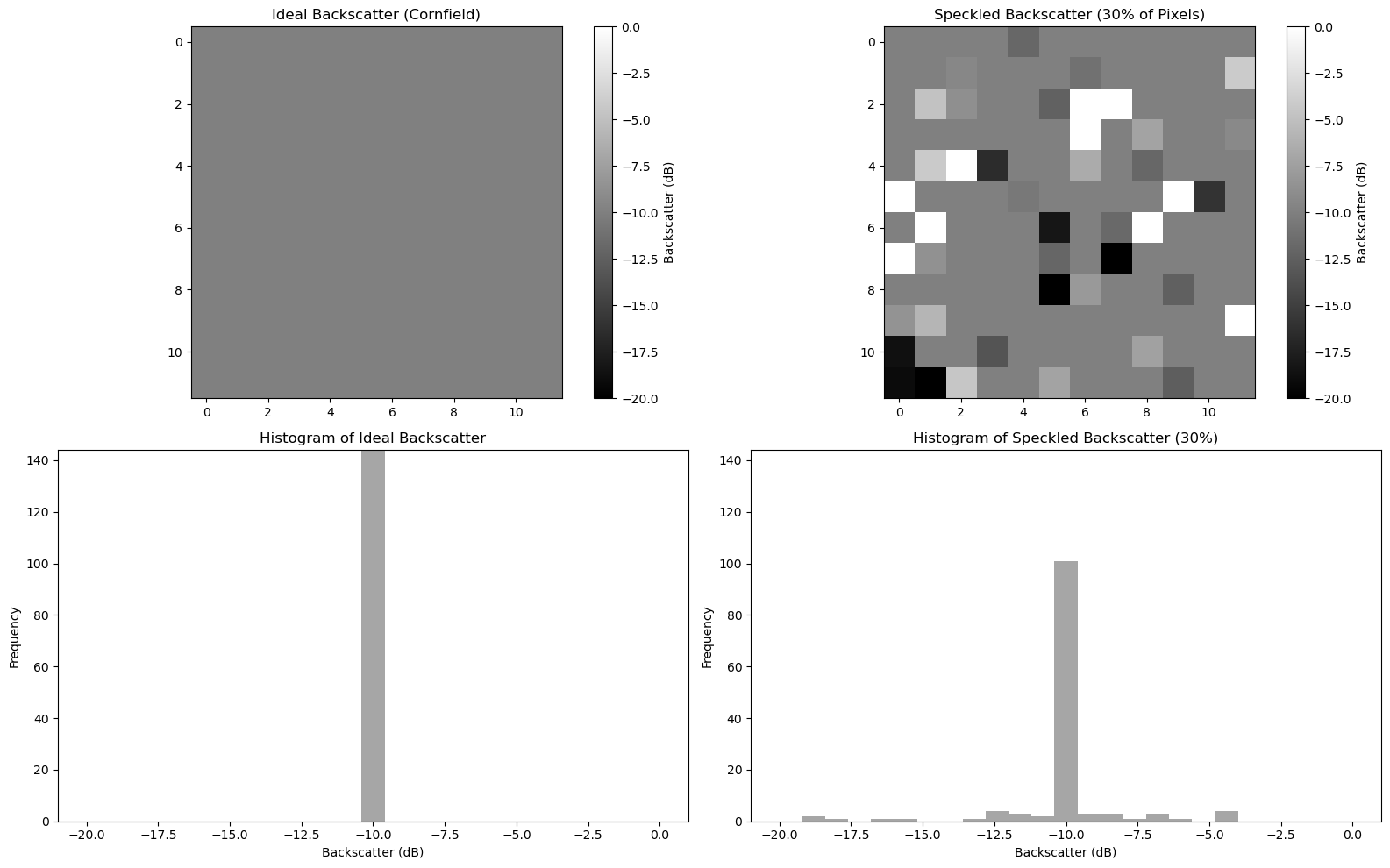
Figure 1: Synthetic data that emulates speckles in microwave backscattering

We can imagine that the second plot represents a real SAR acquisition over a cornfield, while the first plot represents an ideal uniform SAR image over a cornfield land (no speckle). The introduction of a simulated 30% speckle noise could be related to the presence of distributed scatterers of any sort present in the scene, which would cause a pixel-to-pixel variation in terms of intensity.

All the random contributions (such as the wind) would result in a different speckle pattern each time a SAR scene is acquired over the same area. Many subpixel contributors build up a complex scattered pattern in any SAR image, making it erroneous to rely on a single pixel intensity for making reliable image analysis. In order to enhance the degree of usability of a SAR image, several techniques have been put in place to mitigate speckle. We will now show two of the most common approaches: the temporal and the spatial filter.

Lake Neusiedl data

We load a dataset that contains the CORINE land cover and Sentinel-1 \(\sigma^0_E\) at a 20 meter resolution. This is the same data presented in notebook 6.

We also create the same dashboard for backscatter of different landcover types over time. In order to make this code reusable and adaptable we will define the following function plot_variability, which allows the injection of a spatial and/or temporal filter. It is not important to understand all the code of the following cell!

# Load encoding
with cat.corine_cmap.read()[0] as f:
    color_mapping_data = json.load(f)

# Get mapping
color_mapping = {item["value"]: item for item in color_mapping_data["land_cover"]}

# Get landcover codes present in the image
present_landcover_codes = np.unique(
    fused_ds.land_cover.values[~np.isnan(fused_ds.land_cover.values)].astype(int)
)


def load_image(var_ds, time, land_cover, x_range, y_range, filter_fun_spatial=None):
    """
    Callback Function Landcover.

    Parameters
    ----------
    time: panda.datetime
        time slice
    landcover: int
        land cover type
    x_range: array_like
        longitude range
    y_range: array_like
        latitude range

    Returns
    -------
    holoviews.Image
    """

    if time is not None:
        var_ds = var_ds.sel(time=time)

    if land_cover == "\xa0\xa0\xa0 Complete Land Cover":
        sig0_selected_ds = var_ds.sig0
    else:
        land_cover_value = int(land_cover.split()[0])
        mask_ds = var_ds.land_cover == land_cover_value
        sig0_selected_ds = var_ds.sig0.where(mask_ds)

    if filter_fun_spatial is not None:
        sig0_np = filter_fun_spatial(sig0_selected_ds.values)
    else:
        sig0_np = sig0_selected_ds.values

    # Convert unfiltered data into Holoviews Image
    img = hv.Dataset(
        (sig0_selected_ds["x"], sig0_selected_ds["y"], sig0_np), ["x", "y"], "sig0"
    )

    if x_range and y_range:
        img = img.select(x=x_range, y=y_range)

    return hv.Image(img)


def plot_variability(var_ds, filter_fun_spatial=None, filter_fun_temporal=None):

    robust_min = var_ds.sig0.quantile(0.02).item()
    robust_max = var_ds.sig0.quantile(0.98).item()

    bin_edges = [
        i + j * 0.5
        for i in range(int(robust_min) - 2, int(robust_max) + 2)
        for j in range(2)
    ]

    land_cover = {"\xa0\xa0\xa0 Complete Land Cover": 1}
    land_cover.update(
        {
            f"{int(value): 02} {color_mapping[value]['label']}": int(value)
            for value in present_landcover_codes
        }
    )
    time = var_ds.sig0["time"].values

    rangexy = RangeXY()

    if filter_fun_temporal is not None:
        var_ds = filter_fun_temporal(var_ds)
        load_image_ = partial(
            load_image, var_ds=var_ds, filter_fun_spatial=filter_fun_spatial, time=None
        )
        dmap = (
            hv.DynamicMap(load_image_, kdims=["Landcover"], streams=[rangexy])
            .redim.values(Landcover=land_cover)
            .hist(normed=True, bins=bin_edges)
        )

    else:
        load_image_ = partial(
            load_image, var_ds=var_ds, filter_fun_spatial=filter_fun_spatial
        )
        dmap = (
            hv.DynamicMap(load_image_, kdims=["Time", "Landcover"], streams=[rangexy])
            .redim.values(Time=time, Landcover=land_cover)
            .hist(normed=True, bins=bin_edges)
        )

    image_opts = hv.opts.Image(
        cmap="Greys_r",
        colorbar=True,
        tools=["hover"],
        clim=(robust_min, robust_max),
        aspect="equal",
        framewise=False,
        frame_height=500,
        frame_width=500,
    )

    hist_opts = hv.opts.Histogram(width=350, height=555)

    return dmap.opts(image_opts, hist_opts)

Now, lets work on the real-life dataset to see how speckle actually looks like.

plot_variability(fused_ds)