
Spy Keypad
Part 2 for working with audio signals
Overview
A door is encoded with a number pad (0-9). We can’t see the door, but through nefariouis means we have a recording of someone opening it. Quick! We need to decode this mystery signal and the order they appear to open the door!
We know that the door code is set up as:
A note: 0
B note: 1
C note: 2
D note: 3
E note: 4
F note: 5
Prerequisites
Concepts |
Importance |
Notes |
|---|---|---|
Necessary |
Plotting on a data |
|
Necessary |
Familiarity with working with dataframes |
|
Necessary |
Familiarity with working with arrays |
|
Helpful |
Familiarity with working with .wav files |
Time to learn: 30 minutes
Imports
import numpy as np # working with arrays
import pandas as pd # working with dataframes
from scipy.io import wavfile # loading in wav files
import matplotlib.pyplot as plt # plot data
from scipy.fftpack import fft, fftfreq # working with Fourier Transforms
import pywt # PyWavelets
Extract audio .wav file
Like when working with the “Jingle Bells” song file, any .wav input file contains information about the amplitude at every point in the file. The frequency of the note will determine which chord each part of the piece represents
sampleRate, signalData = wavfile.read('../data/mystery_signal.wav')
duration = len(signalData) / sampleRate
time = np.arange(0, duration, 1/sampleRate)
print(f"Sample Rate: {sampleRate}")
print(f"duration = {duration} seconds (sample rate and audioBuffer = {len(signalData)} / {sampleRate})")
print(f"length of audio file = {len(signalData)}")
print(f"Total length in time = {len(time)}")
Sample Rate: 10000
duration = 6.0 seconds (sample rate and audioBuffer = 60000 / 10000)
length of audio file = 60000
Total length in time = 60000
Let’s Give the Data a Look!
It is always good practice to view the data that we have collected. First, let’s organize the data into a pandas dataframe to organize the amplitude and time stamps
signal_df = pd.DataFrame({'time (seconds)': time, 'amplitude': signalData})
signal_df.head()
| time (seconds) | amplitude | |
|---|---|---|
| 0 | 0.0000 | 11182 |
| 1 | 0.0001 | 29148 |
| 2 | 0.0002 | 2847 |
| 3 | 0.0003 | 14564 |
| 4 | 0.0004 | 21618 |
Plot a Small Sample of the .wav File
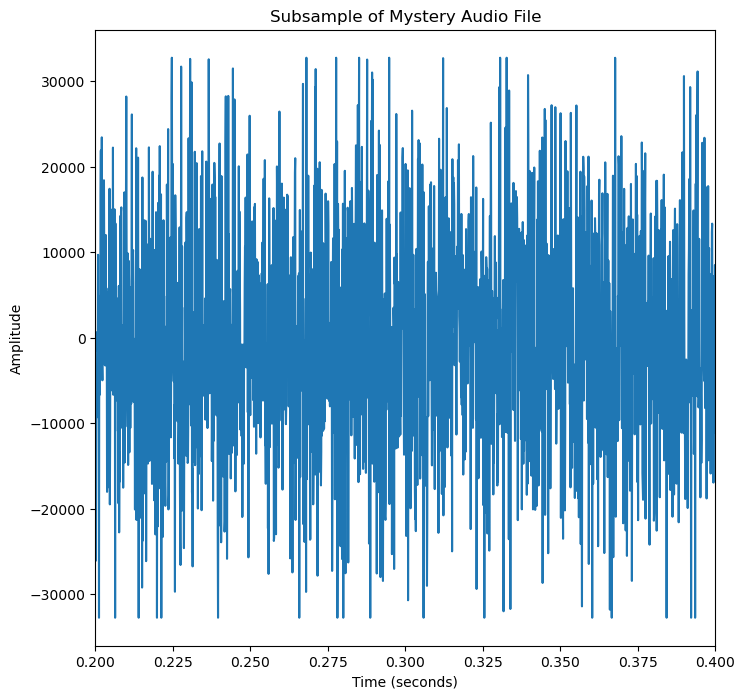
Plot a small subsample of the .wav to visualize the input data
fig, ax = plt.subplots(figsize=(8, 8))
fig = plt.plot(signal_df["time (seconds)"], signal_df["amplitude"])
plt.title("Subsample of Mystery Audio File")
ax.set_xlim(signal_df["time (seconds)"][2000], signal_df["time (seconds)"][4000])
plt.xlabel("Time (seconds)")
plt.ylabel("Amplitude")
plt.show()
Waavelet Analysis: Power Spectrum
The power spectrum plots the real component of the complex number returns from wavelet_coeff. This will return information about the frequency and time that we need to determine which notes are used in what order for the keypad
wavelet_mother = "morl" # morlet
# scale determines how squished or stretched a wavelet is
scales = np.arange(1, 40)
wavelet_coeffs, freqs = pywt.cwt(signalData, scales, wavelet = wavelet_mother)
# Shape of wavelet transform
print(f"size {wavelet_coeffs.shape} with {wavelet_coeffs.shape[0]} scales and {wavelet_coeffs.shape[1]} time steps")
print(f"x-axis be default is: {wavelet_coeffs.shape[1]}")
print(f"y-axis be default is: {wavelet_coeffs.shape[0]}")
size (39, 60000) with 39 scales and 60000 time steps
x-axis be default is: 60000
y-axis be default is: 39
# Plot scalogram
fig, ax = plt.subplots(figsize=(8, 8))
data = np.log2(np.square(abs(wavelet_coeffs))) # compare the magntiude
plt.xlabel("Time Steps")
plt.ylabel("Scale Sensitivity")
plt.imshow(data,
vmax=(data).max(), vmin=(data).min(),
cmap="coolwarm", aspect="auto")
plt.colorbar()
plt.show()
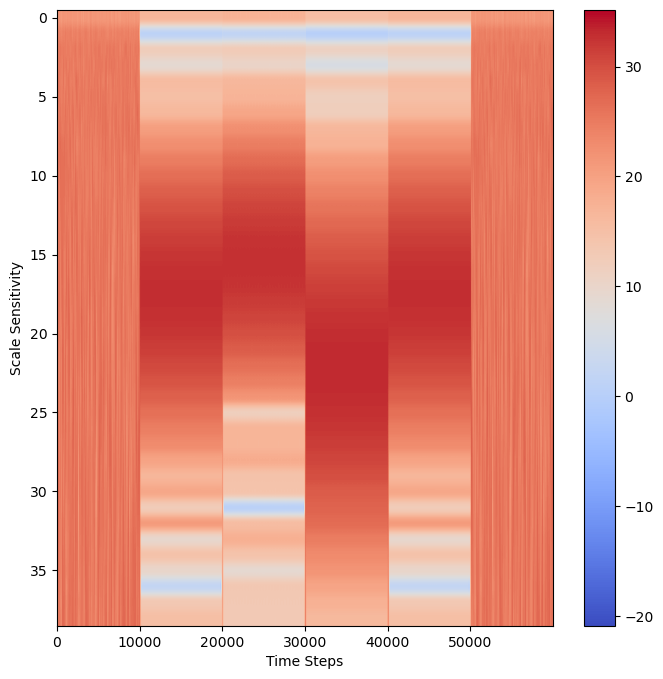
Behold! Distinct Bands of Frequencies!
Each distinct band represents a note. So, we can see that the data at the beginning at the end is random noise, with no distinct frequency. But at 1 second, a distinct note that lasts for 1 second, followed by three additional distinct bands. Let’s see where the possible note frequencies we have might lie on scales
To overlay these frequencies with the wavelet scaologram:
Important Note
To convert HZ frequency to a scale = hz *.0001 (where 0.01 is 100 Hz sampling) then apply frequency2scale PyWavelets function
fig, ax = plt.subplots(figsize=(8, 8))
# Overlay frequency of notes as dotted lines
sample_rate = 1/sampleRate
a_freq = pywt.frequency2scale(wavelet_mother, 440*sample_rate)
plt.axhline(y=a_freq, color='cyan', linestyle='--', label='A')
b_freq = pywt.frequency2scale(wavelet_mother, 494*sample_rate)
plt.axhline(y=b_freq, color="green", linestyle='--', label='B')
c_freq = pywt.frequency2scale(wavelet_mother, 261*sample_rate)
plt.axhline(y=c_freq, color='brown', linestyle='--', label='C')
d_freq = pywt.frequency2scale(wavelet_mother, 293*sample_rate)
plt.axhline(y=d_freq, color='orange', linestyle='--', label='D')
e_freq = pywt.frequency2scale(wavelet_mother, 330*sample_rate)
plt.axhline(y=e_freq, color='indigo', linestyle='--', label='E')
f_freq = pywt.frequency2scale(wavelet_mother, 350*sample_rate)
plt.axhline(y=f_freq, color='red', linestyle='--', label='F')
# Plot Power scalogram
power = np.log2(np.square(abs(wavelet_coeffs))) # compare the magntiude
plt.title("Note Frequency as Scale")
plt.xlabel("Time Steps")
plt.ylabel("Scale Sensitivity")
plt.imshow(power,
vmax=(power).max(), vmin=(power).min(),
cmap="coolwarm", aspect="auto")
plt.legend()
plt.show()
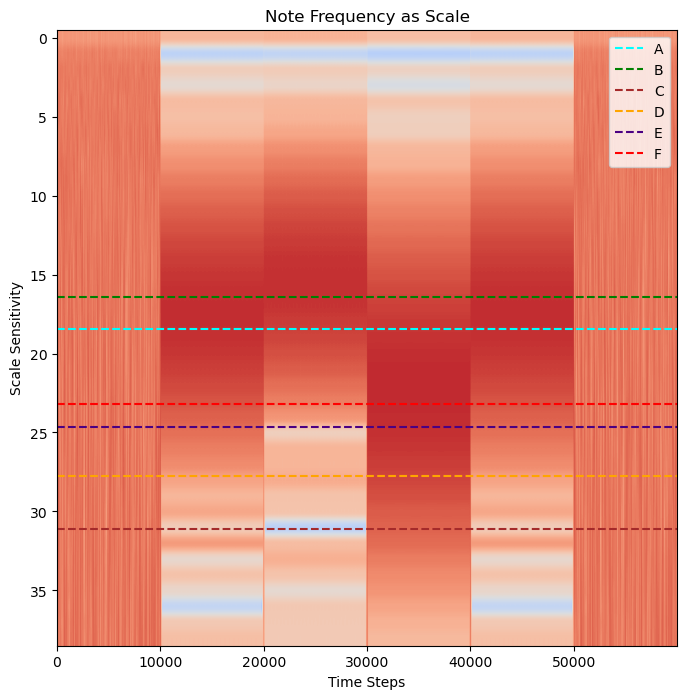
But Which Match Best?
We are looking for a note frequency that best lines up with the darkest part of each band. The first and the last band seem like the same note, but is it closer to an A note or a B note?
Let’s see if we can use Fourier Transform to get a smaller range of notes to chose from
Fast Fourier Transform
fourier_transform = abs(fft(signalData))
freqs = fftfreq(len(fourier_transform), sample_rate)
fig, ax = plt.subplots(figsize=(8, 8))
plt.plot(freqs, fourier_transform)
ax.set_xlim(left=200, right=500)
plt.axvline(x=440, color="cyan", label="A",alpha=0.5) # A note: 440 hz
plt.axvline(x=494, color="green", label="B",alpha=0.5) # B Note: 494 hz
plt.axvline(x=261, color="brown", label="C",alpha=0.5) # C Note: 261 hz
plt.axvline(x=293, color="orange", label="D",alpha=0.5) # D Note: 293 hz
plt.axvline(x=330, color="indigo", label="E",alpha=0.5) # E Note: 330 hz
plt.axvline(x=350, color="red", label="F",alpha=0.5) # F Note: 350 hz
plt.title("Signal Frequency Prevalence (FFT)")
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.legend()
plt.show()
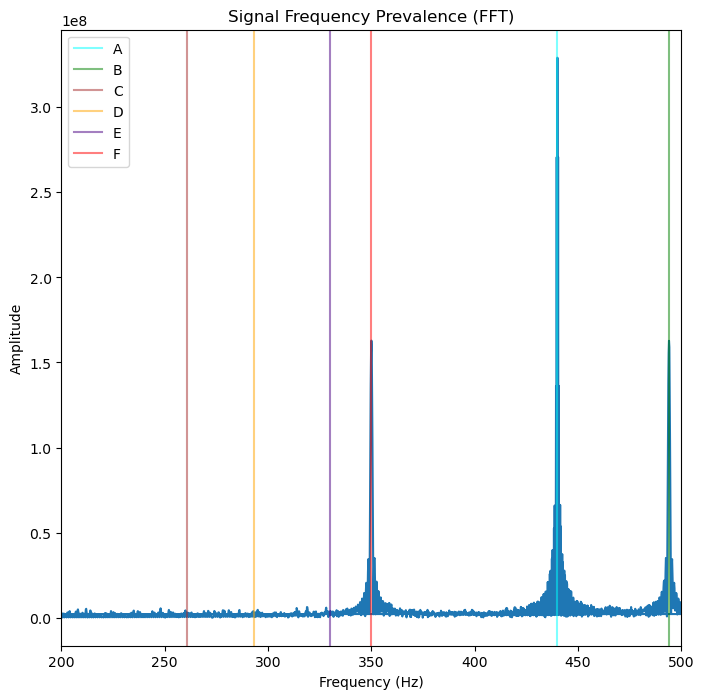
Perfect, There are Three Notes!
Three notes stand out, and one note is used about twice as much as the other two: A, B, F
fig, ax = plt.subplots(figsize=(8, 8))
# Overlay frequency of notes as dotted lines
sample_rate = 1/sampleRate
a_freq = pywt.frequency2scale(wavelet_mother, 440*sample_rate)
plt.axhline(y=a_freq, color='cyan', linestyle='--', label='A')
b_freq = pywt.frequency2scale(wavelet_mother, 494*sample_rate)
plt.axhline(y=b_freq, color="green", linestyle='--', label='B')
f_freq = pywt.frequency2scale(wavelet_mother, 350*sample_rate)
plt.axhline(y=f_freq, color='blue', linestyle='--', label='F')
# Plot Power scalogram
power = np.log2(np.square(abs(wavelet_coeffs))) # compare the magntiude
plt.title("Note Frequency as Scale")
plt.xlabel("Time Steps")
plt.ylabel("Scale Sensitivity")
plt.imshow(power,
vmax=(power).max(), vmin=(power).min(),
cmap="coolwarm", aspect="auto")
plt.legend()
plt.show()
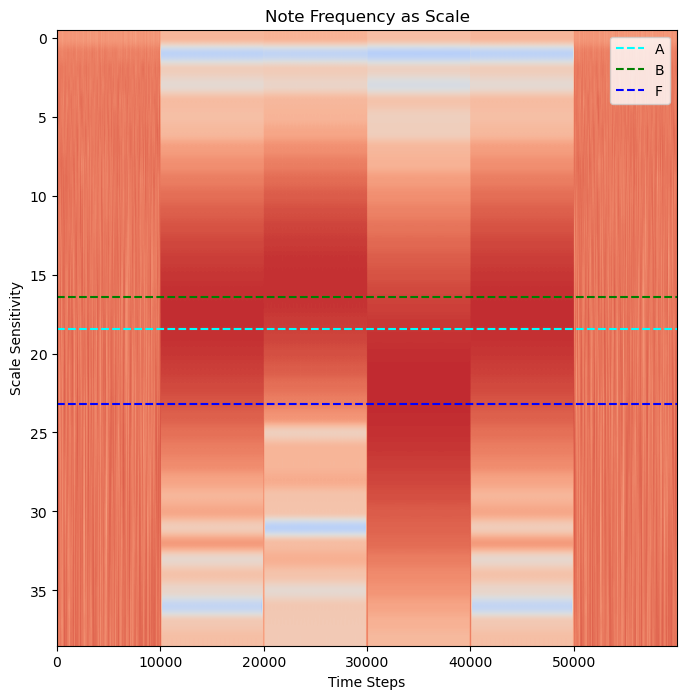
Three Notes Played Over Six Seconds
We have the keypad solution! The three notes are played (sometimes repeated) over the course of the six seconds
A, B, F, A
From our original problem, we know that the door code is set up as:
A note: 0
B note: 1
C note: 2
D note: 3
E note: 4
F note: 5
The solution to the door password is:
0, 1, 5, 0
Summary
Now we’ve had a chance to work with unknown input values, but within an expected range. Different time-series data will have different ranges of expected frequencies, and with Fourier Transform and wavelet analysis it is possible to pull out such relevant data.
What’s next?
Up next: apply wavelets transform and work with weather data!
